题目内容
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和最低点分别为(x0 , 2),(x0+
)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和最低点分别为(x0 , 2),(x0+ ![]() ,﹣2).
,﹣2).
(1)求函数y=f(x)的解析式和单调递增区间;
(2)若当0≤x≤ ![]() 时,方程f(x)﹣m=0有两个不同的实数根α,β,试讨论α+β的值.
时,方程f(x)﹣m=0有两个不同的实数根α,β,试讨论α+β的值.
【答案】
(1)解:由题意可得:A=2,
由在y轴右侧的第一个最高点和最低点分别为(x0,2),(x0+ ![]() ,﹣2),可得:
,﹣2),可得:
![]() =(x0+
=(x0+ ![]() )﹣x0=
)﹣x0= ![]() ,可得:T=π,
,可得:T=π,
∴ω=2,可得:f(x)=2sin(x+φ),
又∵图象与y轴的交点为(0,1),可得:2sinφ=1,解得:sinφ= ![]() ,
,
∵|φ|< ![]() ,可得:φ=
,可得:φ= ![]() ,
,
∴函数f(x)的解析式为:f(x)=2sin(2x+ ![]() )
)
由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,可得:kπ﹣
,k∈Z,可得:kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
可解得f(x)的单调递增区间是:[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
(2)解:如图所示,在同一坐标系中画出y=2sin(2x+ ![]() )和y=m(m∈R)的图象,
)和y=m(m∈R)的图象,
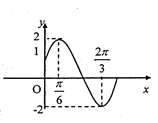
由图可知,当﹣2<m≤0或1≤m<2时,直线y=m与曲线有两个不同的交点,即原方程有两个不同的实数根,
当﹣2<m≤0时,两根和为 ![]() ;
;
当1≤m<2时,两根和为 ![]()
【解析】(1)由函数的图象的顶点坐标求出A,由周期求出ω,由图象与y轴的交点为(0,1)求出φ的值,可得函数的解析式,利用正弦函数的单调性可求单调递增区间;(2)在同一坐标系中画出y=2sin(2x+ ![]() )和直线y=m(m∈R)的图象,结合正弦函数的图象的特征,数形结合求得实数m的取值范围和这两个根的和.
)和直线y=m(m∈R)的图象,结合正弦函数的图象的特征,数形结合求得实数m的取值范围和这两个根的和.

练习册系列答案
相关题目