题目内容
【题目】如图,在三棱锥P﹣ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC. (Ⅰ)求直线PC与平面ABC所成角的大小;
(Ⅱ)求二面角B﹣AP﹣C的大小.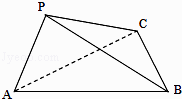
【答案】解法一 (Ⅰ)设AB中点为D,AD中点为O,连接OC,OP,CD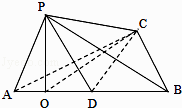
因为AB=BC=CA,所以CD⊥AB,
因为∠APB=90°,∠PAB=60°,所以△PAD为等边三角形,所以PO⊥AD,又平面PAB⊥平面ABC,平面PAB∩平面ABC=AD.
PO⊥平面ABC,∠OCP为直线PC与平面ABC所成的角
不妨设PA=2,则OD=1,OP= ![]() ,AB=4.
,AB=4.
所以CD=2 ![]() ,OC=
,OC= ![]() =
= ![]() =
= ![]()
在RT△OCP中,tan∠OCP= ![]() =
= ![]() =
= ![]() .
.
故直线PC与平面ABC所成的角的大小为arctan ![]() .
.
(Ⅱ)过D作DE⊥AP于E,连接CE.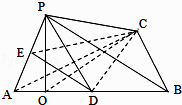
由已知,可得CD⊥平面PAB.根据三垂线定理知,CE⊥PA.所以∠CED为二面角
B﹣AP﹣C的平面角.由(Ⅰ)知,DE= ![]() ,在RT△CDE中,tan∠CED=
,在RT△CDE中,tan∠CED= ![]() =
= ![]() =2,故二面角B﹣AP﹣C的大小为arctan2.
=2,故二面角B﹣AP﹣C的大小为arctan2.
解法二:(Ⅰ)设AB中点为D,连接CD.因为O在AB上,且O为P在平面ABC内的射影,
所以PO⊥平面ABC,所以PO⊥AB,且PO⊥CD.因为AB=BC=CA,所以CD⊥AB,设E为AC中点,则EO∥CD,从而OE⊥PO,OE⊥AB.
如图,以O为坐标原点,OB,OE,OP所在直线分别为x,y,z轴建立空间直角坐标系O﹣xyz.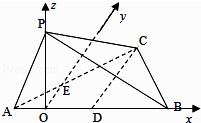
不妨设PA=2,由已知可得,AB=4,OA=OD=1,OP= ![]() ,
,
CD=2 ![]() ,所以O(0,0,0),A(﹣1,0,0),C(1,2
,所以O(0,0,0),A(﹣1,0,0),C(1,2 ![]() ,0),P(0,0,
,0),P(0,0, ![]() ),所以
),所以 ![]() =(﹣1,﹣2
=(﹣1,﹣2 ![]() ,
, ![]() )
) ![]() =(0,0,
=(0,0, ![]() )为平面ABC的一个法向量.
)为平面ABC的一个法向量.
设α为直线PC与平面ABC所成的角,则sinα= 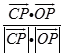 =
= ![]() =
= ![]() .故直线PC与平面ABC所成的角大小为arcsin
.故直线PC与平面ABC所成的角大小为arcsin ![]()
(Ⅱ)由(Ⅰ)知, ![]() =(1,0,
=(1,0, ![]() ),
), ![]() =(2,2
=(2,2 ![]() ,0).
,0).
设平面APC的一个法向量为 ![]() =(x,y,z),则由
=(x,y,z),则由 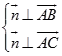 得出
得出 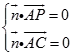 即
即  ,
,
取x=﹣ ![]() ,则y=1,z=1,所以
,则y=1,z=1,所以 ![]() =(﹣
=(﹣ ![]() ,1,1).设二面角B﹣AP﹣C的平面角为β,易知β为锐角.
,1,1).设二面角B﹣AP﹣C的平面角为β,易知β为锐角.
而面ABP的一个法向量为 ![]() =(0,1,0),则cosβ=
=(0,1,0),则cosβ= ![]() =
= ![]() =
= ![]() .
.
故二面角B﹣AP﹣C的大小为arccos ![]() .
.
【解析】解法一(Ⅰ)设AB中点为D,AD中点为O,连接OC,OP,CD.可以证出∠OCP为直线PC与平面ABC所成的角.不妨设PA=2,则OD=1,OP= ![]() ,AB=4.在RT△OCP中求解.(Ⅱ)以O为原点,建立空间直角坐标系,利用平面APC的一个法向量与面ABP的一个法向量求解. 解法二(Ⅰ)设AB中点为D,连接CD.以O为坐标原点,OB,OE,OP所在直线分别为x,y,z轴建立空间直角坐标系O﹣xyz.利用
,AB=4.在RT△OCP中求解.(Ⅱ)以O为原点,建立空间直角坐标系,利用平面APC的一个法向量与面ABP的一个法向量求解. 解法二(Ⅰ)设AB中点为D,连接CD.以O为坐标原点,OB,OE,OP所在直线分别为x,y,z轴建立空间直角坐标系O﹣xyz.利用 ![]() 与平面ABC的一个法向量夹角求解.(Ⅱ)分别求出平面APC,平面ABP的一个法向量,利用两法向量夹角求解.
与平面ABC的一个法向量夹角求解.(Ⅱ)分别求出平面APC,平面ABP的一个法向量,利用两法向量夹角求解.
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 ,以及对用空间向量求直线与平面的夹角的理解,了解设直线
,以及对用空间向量求直线与平面的夹角的理解,了解设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: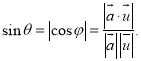 .
.

 智慧小复习系列答案
智慧小复习系列答案【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销 ![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(1)求 ![]() 关于
关于 ![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.