题目内容
已知函数 .
.
(Ⅰ)若函数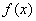 在
在 上是增函数,求正实数
上是增函数,求正实数 的取值范围;
的取值范围;
(Ⅱ)若 ,
, 且
且 ,设
,设 ,求函数
,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当 时,
时, ,
, ;当
;当 且
且 时,
时, ,
, .
.
 (i)若
(i)若 ,在
,在 上,恒有
上,恒有 ,所以
,所以 在
在 上单调递减,
上单调递减,

 …………10分
…………10分
(ii) 时,因为
时,因为 ,所以
,所以 ,
, ,所以
,所以 ,
,
所以 在
在 上单调递减
上单调递减

 …………12分
…………12分
综上所述:当 时,
时, ,
, ;
;
当 且
且 时,
时, ,
, .…………13分
.…………13分
考点:1.利用函数的单调性求函数的最值;2.化归转化和分类讨论的数学思想方法的运用

练习册系列答案
相关题目
 无实根,则双曲线
无实根,则双曲线 的离心率的取值范围为
的离心率的取值范围为 .
.  的定义域是 .
的定义域是 . 解集为空集,则满足条件的实数a的值为 .
解集为空集,则满足条件的实数a的值为 .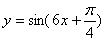 图象上各点的横坐标伸长到原来的3倍,再向右平移
图象上各点的横坐标伸长到原来的3倍,再向右平移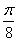 个单位,得到的函数的一个对称中心是( )
个单位,得到的函数的一个对称中心是( )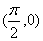 B.
B.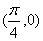 C.
C.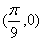 D.
D.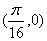
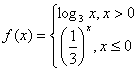 ,则满足方程
,则满足方程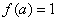 的所有的
的所有的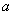 的值为 .
的值为 .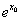 ≤0 (B)∀x∈R, 2x>x2
≤0 (B)∀x∈R, 2x>x2 的离心率为
的离心率为
 的渐近线方程为
的渐近线方程为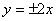
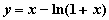 的单调递增区间是
的单调递增区间是