题目内容
3．已知x，y＞0，且x2+y2=1，则x+y的最大值等于$\sqrt{2}$．分析 由已知条件可得1≥$\frac{1}{2}$（x+y）2，即可求出
解答 解：x＞，y＞0，且1=x2+y2=（x+y）2-2xy≥（x+y）2-2（$\frac{x+y}{2}$）2=$\frac{1}{2}$（x+y）2，当且仅当x=y=$\frac{\sqrt{2}}{2}$时取等号
∴（x+y）2≤2，
∴0＜x+y≤$\sqrt{2}$，
∴x+y的最大值等于$\sqrt{2}$，
故答案为：$\sqrt{2}$．
点评 本题考查了基本不等式的应用，属于基础题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．若函数f（x）=（x-2）ex+a（x-1）2，（a＞0）存在负数零点，则a的取值范围是（ ）
| A． | （2，+∞） | B． | （2，6） | C． | （0，6） | D． | （0，2） |
11．45°=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
18．如图所示的韦恩图中，全集U=R，若A={x|0≤x＜2}，B={x|x＞1}，则阴影部分表示的集合为（ ）
| A． | {x|x＞1} | B． | {x|1＜x＜2} | C． | {x|x＞2} | D． | {x|x≥2} |
12．已知a＞0，b＞0，$\frac{1}{a}$$+\frac{3}{b}$=2，则a+2b的最小值为（ ）
| A． | 7+2$\sqrt{6}$ | B． | $\frac{7}{2}$+$\sqrt{6}$ | C． | 5$+2\sqrt{6}$ | D． | $\frac{5}{2}+\sqrt{6}$ |
12．如图，α-MN-β为120°，O∈MN，a∈β，B∈α．∠BON=∠AOM=45°，$OA=OB=\sqrt{2}$，则AB=（ ）
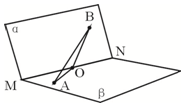
| A． | $\sqrt{5}$ | B． | $2\sqrt{3}$ | C． | $\sqrt{6}$ | D． | $\sqrt{7}$ |