题目内容
已知点（4，2）是直线l被椭圆
+
=1所截得的线段的中点，则直线l的斜率是
| x2 |
| 36 |
| y2 |
| 9 |
-
| 1 |
| 2 |
-
．| 1 |
| 2 |
分析：设l与椭圆的交点为A（x1，y1），B（x2，y2），通过平方差法，求出直线l的斜率．
解答：解：因为点（4，2）是直线l被椭圆
+
=1所截得的线段的中点，
设l与椭圆的交点为A（x1，y1），B（x2，y2），
则有
，
两式相减，得kAB=
=--
=-
，
直线l的斜率是-
故答案为：-
．
| x2 |
| 36 |
| y2 |
| 9 |
设l与椭圆的交点为A（x1，y1），B（x2，y2），
则有
|
两式相减，得kAB=
| y1-y2 |
| x1-x2 |
| 9(x1+x2) |
| 36(y1+y2) |
| 1 |
| 2 |
直线l的斜率是-
| 1 |
| 2 |
故答案为：-
| 1 |
| 2 |
点评：本题考查椭圆的中点弦的求法，解题时要注意点差法的合理运用．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
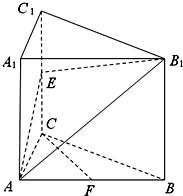如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，E是棱CC1上动点，F是AB中点，AC=BC=2，AA1=4．
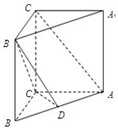如图，已知直三棱柱ABC-A1B1C1中，AB=5，AC=4，BC=3，AA1=4，点D在AB上．
如图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=B1C1=2，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3．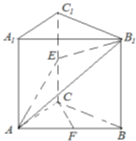
（2013•渭南二模）如图，已知直三棱柱ABC-A1B1C1中，∠ACB=90°，E是棱CC1上的动点，F是AB的中点，AC=BC=2，AA1=4．