Question

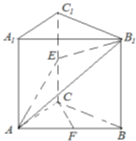（2013•渭南二模）如图，已知直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，E是棱CC₁上的动点，F是AB的中点，AC=BC=2，AA₁=4．
（1）当E是棱CC₁的中点时，求证：CF∥平面AEB₁；
（2）在棱CC₁上是否存在点E，使得二面角A-EB₁-B的大小是45°？若存在，求出CE的长，若不存在，请说明理由．

Answer 1

分析：（1）取AB₁中点M，连接EM、FM，在△AB₁B中根据中位线定理，得MF∥B₁B且MF=

1

2

B₁B，在矩形BB₁C₁C中，CE∥B₁B且CE=

1

2

B₁B，得到四边形MFCE是平行四边形，CF∥EM，从而证出CF∥平面AEB₁；
（2）以CA、CB、CC₁为x、y、z轴，建立空间直角坐标系，设CE=m，得到A、B₁和E各点的坐标，根据垂直向量的数量积为零的方法列方程组并解之，得到平面AEB₁的法向量为

n

=（m，m-4，2），再由题意得到平面AEB₁的法向量和平面EB₁B的法向量夹角的余弦绝对值为

2

2

，由此建立关系式，可解出m=

5

2

，从而得出存在点满足条件的点E．

解答：解：（1）取AB₁中点M，连接EM、FM-----------------（1分）
∵△AB₁B中，M、F分别是AB、AB₁的中点，
∴MF∥B₁B且MF=

1

2

B₁B，
又∵矩形BB₁C₁C中，CE∥B₁B且CE=

1

2

B₁B，
∴MF∥CE且MF=CE，可得四边形MFCE是平行四边形-------------（4分）
∴CF∥EM
∵CF?平面EAB₁，EM⊆平面EAB₁，
∴CF∥平面AEB₁----------------------（6分）
（2）以CA、CB、CC₁为x、y、z轴，建立如图空间直角坐标系，
可得A（2，0，0），B₁（0，2，4），设CE=m，得E（0，0，m）
∴

AE

=（-2，0，m），

AB1

=（-2，2，4）
设平面AEB₁的法向量为

n

=（x，y，z）
则有

AE • n =-2x+mz=0 AB1 =-2x+2y+4z=0

，解之并取z=2，得

n

=（m，m-4，2）

∵平面EB₁B的法向量为

CA

=（2，0，0），-------------------（8分）
∴当二面角A-EB₁-B的大小是45°时，有
cos＜

n

，

CA

＞=

2m

m2+(m-4)2+4 •2

=

2

2

，解之得m=

5

2

．
因此，在棱CC₁上存在点E，当CE=

5

2

时，二面角A-EB₁-B的大小是45°．-------------（12分）

点评：本题在直三棱柱中，求证线面平行并探索二面角的大小能否为45度，着重考查了直线与平面垂直的判定、用空间向量研究二面角的大小等知识点，属于中档题．