题目内容
点 关于直线
关于直线 的对称点是
的对称点是 ,则直线
,则直线 在
在 轴上的截距是( )
轴上的截距是( )
A. | B. | C.  | D. |
A
解析试题分析:由题意知,结合点关于直线对称可知,一个是直线垂直,同时两点的中点在对称轴上,因此
∴直线方程为 其在x轴上的截距为
其在x轴上的截距为 ,故选A.
,故选A.
考点:本题主要是考查与直线关于点、直线对称的直线方程、直线的截距、方程组的解法等基础知识,考查运算求解能力.属于基础题.
点评:解决该试题的关键是点关于直线对称,可以根据对称点的坐标,利用两点连线的斜率与直线垂直.然后两点中点在直线上.联立两个一元两次方程即可求解出直线方程,最后令y=0求出在x轴上的截距

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线 的倾斜角是( )
的倾斜角是( )
| A.300 | B.600 | C.1200 | D.1350 |
若直线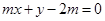 与直线
与直线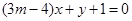 垂直,则
垂直,则 的值是( )
的值是( )
A.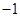 或 或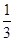 | B.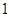 或 或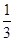 | C.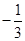 或 或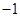 | D.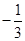 或1 或1 |
经过两点(3,9)、(-1,1)的直线在x轴上的截距为
A.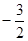 | B.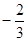 | C.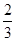 | D.2 |
过点(1,0)且与直线 平行的直线方程是( )
平行的直线方程是( )
A. | B. |
C. | D. |
( )由直线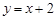 上的一点向圆
上的一点向圆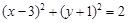 引切线,则切线长的最小值为
引切线,则切线长的最小值为
A.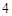 | B.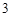 | C.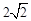 | D. |
已知点 在直线
在直线 上,则
上,则 的最小值是( )
的最小值是( )
| A.4 | B.6 | C.8 | D.9 |
直线与函数 的图像相切于点
的图像相切于点 ,且
,且 ,
, 为坐标原点,
为坐标原点, 为图像的极大值点,与
为图像的极大值点,与 轴交于点
轴交于点 ,过切点
,过切点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,则
,则 =
=
A. | B. | C. | D. 2 |
与直线 平行的抛物线
平行的抛物线 的切线方程是( )
的切线方程是( )
A. | B. |
C. | D. |