题目内容
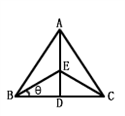
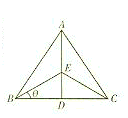 某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在位于∠BAC的角平分线上的选址E处(记∠EBD=θ),修建一农副产品加工厂,要求使得E到三村的中敦f(θ)尽可能的小.
某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在位于∠BAC的角平分线上的选址E处(记∠EBD=θ),修建一农副产品加工厂,要求使得E到三村的中敦f(θ)尽可能的小.
(1)试求出f(θ)关于θ的函数关系式;
(2)间θ为何值时,f(θ)最小?试述理由.
解:(1)由题意得 ,
, ,
,
∴
∴f(θ)=2BE+ a-ED=
a-ED= (0≤θ≤
(0≤θ≤ );
);
(2)构造函数 (0≤θ≤
(0≤θ≤ ),
),
∴ (0≤θ≤
(0≤θ≤ );
);
令g′(θ)=0,可得sinθ= ,
,
∵0≤θ≤ ,∴θ=
,∴θ=
当0≤θ< 时,g′(θ)<0,函数单调递减,
时,g′(θ)<0,函数单调递减,
当 <θ≤
<θ≤ 时,g′(θ)>0,函数单调递增
时,g′(θ)>0,函数单调递增
所以θ= 时,
时, 取得最小值
取得最小值
因为a>0,所以 取得最小值时,f(θ)最小为
取得最小值时,f(θ)最小为 a,此时θ=
a,此时θ=
分析:(1)利用θ表示BE、ED,进而可得f(θ)关于θ的函数关系式;
(2)构造函数 (0≤θ≤
(0≤θ≤ ),求导函数,求得θ=
),求导函数,求得θ= 时,
时, 取得最小值,从而可得f(θ)最小值及θ的值.
取得最小值,从而可得f(θ)最小值及θ的值.
点评:本题考查利用导数知识解决实际问题,考查函数模型的确立,解题的关键是利用导数求得函数的单调性与最值.
 ,
, ,
,∴

∴f(θ)=2BE+
 a-ED=
a-ED= (0≤θ≤
(0≤θ≤ );
);(2)构造函数
 (0≤θ≤
(0≤θ≤ ),
),∴
 (0≤θ≤
(0≤θ≤ );
);令g′(θ)=0,可得sinθ=
 ,
,∵0≤θ≤
 ,∴θ=
,∴θ=
当0≤θ<
 时,g′(θ)<0,函数单调递减,
时,g′(θ)<0,函数单调递减,当
 <θ≤
<θ≤ 时,g′(θ)>0,函数单调递增
时,g′(θ)>0,函数单调递增所以θ=
 时,
时, 取得最小值
取得最小值
因为a>0,所以
 取得最小值时,f(θ)最小为
取得最小值时,f(θ)最小为 a,此时θ=
a,此时θ=
分析:(1)利用θ表示BE、ED,进而可得f(θ)关于θ的函数关系式;
(2)构造函数
 (0≤θ≤
(0≤θ≤ ),求导函数,求得θ=
),求导函数,求得θ= 时,
时, 取得最小值,从而可得f(θ)最小值及θ的值.
取得最小值,从而可得f(θ)最小值及θ的值.点评:本题考查利用导数知识解决实际问题,考查函数模型的确立,解题的关键是利用导数求得函数的单调性与最值.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
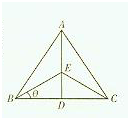 某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在位于∠BAC的角平分线上的选址E处(记∠EBD=θ),修建一农副产品加工厂,要求使得E到三村的中敦f(θ)尽可能的小.
某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在位于∠BAC的角平分线上的选址E处(记∠EBD=θ),修建一农副产品加工厂,要求使得E到三村的中敦f(θ)尽可能的小.