题目内容
已知f′（x0）=a，则
的值为（ ）
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| 2△x |
分析：根据f′（x0）=a，再由
=a，且
与
的关系，通过运算求得结果．
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| 2△x |
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
解答：解：若f（x0）=a，则
=a，
又
=2
=2
=2f（x0）=2a，
故选B．
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
又
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| 2△x |
=2
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| 4△x |
=2
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
=2f（x0）=2a，
故选B．
点评：本题主要考查函数在x0处的极限的定义，式子的变形，是解题的关键，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
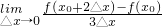的值是
