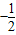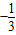题目内容
已知实数a,b满足等式(
)a=(
)b,写出满足条件的一个关系式
| 1 |
| 2 |
| 1 |
| 3 |
a=b=0或a=blog
或b=alog
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
a=b=0或a=blog
或b=alog
.
(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
分析:根据指数函数的性质,利用取对数法求a,b之间的关系即可.
解答:解:①当a=b=0时,(
)a=(
)b=1,等式成立.
②在等式的两边取
为底的对数,得log
(
)a=log
(
)b,即a=blog
.
③在等式的两边取
为底的对数,得log
(
)a=log
(
)b,即b=alog
.
故答案:a=b=0或a=blog
或b=alog
.
| 1 |
| 2 |
| 1 |
| 3 |
②在等式的两边取
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
③在等式的两边取
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
故答案:a=b=0或a=blog
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题主要考查指数函数的基本运算,利用取对数法是解决指数方程中最常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数a、b满足条件:ab<0,且1是a2与b2的等比中项,又是
,
的等差中项,则
的值是( )
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
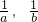 的等差中项,则
的等差中项,则 的值是
的值是



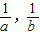 的等差中项,则
的等差中项,则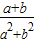 的值是( )
的值是( )