题目内容
求下列关于x的函数的定义域和值域：
(1)y=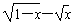
；
(2)y=log2(-x2+2x)；
(3)
。
(1)y=
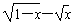；(2)y=log2(-x2+2x)；
(3)
。解：(1)要使函数有意义，则
，
∴0≤x≤1，函数的定义域为[0，1]．
∵函数y=
为减函数，
∴函数的值域为[-1，1]．
(2)要使函数有意义，则-x2+2x＞0，
∴0＜x＜2，∴函数的定义域为(0，2)．
又∵当x∈(0，2)时，-x2+2x∈(0，1]，
∴log2(-x2+2x)∈(-∞，0]，
即函数的值域为(-∞，0]．
(3)函数定义域为{0，1，2，3，4，5}，
函数值域为{2，3，4，5，6，7}．
练习册系列答案
相关题目
－
；求下列关于x的函数的定义域和值域：
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 5 | 6 | 7 |
求下列关于x的函数的定义域和值域：
(1)y＝
－
；
(2)y＝log2(－x2＋2x)；
(3)
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 5 | 6 | 7 |