题目内容
已知平面上的点集E={(x,y)|
},F={(x,y)|x2+y2-2x-2y≤0},若“点P∈E”是“点P∈F”的充分不必要条件,则实数k的取值范围是( )
|
分析:确定平面上的点集,集合F表示的图形,由“点P∈E”是“点P∈F”的充分不必要条件,建立不等式,即可求得k的取值范围.
解答: 解:平面上的点集E={(x,y)|
解:平面上的点集E={(x,y)|
}表示一个三角形区域,F={(x,y)|x2+y2-2x-2y≤0}表示一个圆面(包含边界),
由
得
∵“点P∈E”是“点P∈F”的充分不必要条件,
∴(
)2+(
)2-2×
-2×
≤0
∴k(k-3)≤0
∴0≤k≤3
故选B.
 解:平面上的点集E={(x,y)|
解:平面上的点集E={(x,y)|
|
由
|
|
∵“点P∈E”是“点P∈F”的充分不必要条件,
∴(
| 4 |
| 2+k |
| 4k |
| 2+k |
| 4 |
| 2+k |
| 4k |
| 2+k |
∴k(k-3)≤0
∴0≤k≤3
故选B.
点评:本题考查线性规划知识,考查数形结合的数学思想,考查解不等式,属于中档题.

练习册系列答案
相关题目
 在A,B,C,D四小题中只能选做2题,每题10分,共计20分.
在A,B,C,D四小题中只能选做2题,每题10分,共计20分.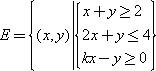 ,F={(x,y)|x2+y2-2x-2y≤0},若“点P∈E”是“点P∈F”的充分不必要条件,则实数k的取值范围是
,F={(x,y)|x2+y2-2x-2y≤0},若“点P∈E”是“点P∈F”的充分不必要条件,则实数k的取值范围是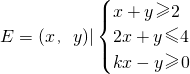 ,F={(x,y)|x2+y2-2x-2y≤0},若“点P∈E”是“点P∈F”的充分不必要条件,则实数k的取值范围是
,F={(x,y)|x2+y2-2x-2y≤0},若“点P∈E”是“点P∈F”的充分不必要条件,则实数k的取值范围是 ,F={(x,y)|x2+y2-2x-2y≤0},若“点P∈E”是“点P∈F”的充分不必要条件,则实数k的取值范围是( )
,F={(x,y)|x2+y2-2x-2y≤0},若“点P∈E”是“点P∈F”的充分不必要条件,则实数k的取值范围是( )