题目内容
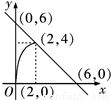
 求由抛物线y2=8x(y>0)与直线x+y-6=0及y=0所围成图形的面积.
求由抛物线y2=8x(y>0)与直线x+y-6=0及y=0所围成图形的面积.
分析:根据定积分的定义结合图象可得,S=
2
•
dx+
(6-x)dx,然后利用定积分的定义进行计算.
| ∫ | 2 0 |
| 2 |
| x |
| ∫ | 6 2 |
解答:解:设所求图形面积为S,S=
2
•
dx+
(6-x)dx(4分)
=
x
+(6x-
x2)
(8分)
=
+8=
(12分)
| ∫ | 2 0 |
| 2 |
| x |
| ∫ | 6 2 |
=
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| | | 2 0 |
| 1 |
| 2 |
| | | 6 2 |
=
| 16 |
| 3 |
| 40 |
| 3 |
点评:此题考查利用定积分求图形的面积问题,解题的关键是将图象的面积分为两部分进行处理.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
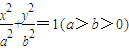 的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.
的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.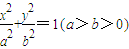 的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.
的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.