题目内容
已知数列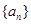 满足
满足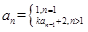 ,则(1)当
,则(1)当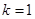 时,求数列
时,求数列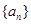 的前
的前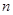 项和
项和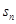 ;(2)当
;(2)当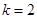 时,证明数列
时,证明数列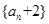 是等比数列。
是等比数列。
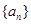 满足
满足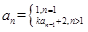 ,则(1)当
,则(1)当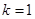 时,求数列
时,求数列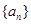 的前
的前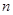 项和
项和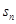 ;(2)当
;(2)当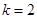 时,证明数列
时,证明数列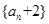 是等比数列。
是等比数列。(1)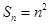
(2)证得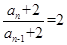 ,数列
,数列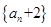 是以
是以 为首项,公比为2的等比数列
为首项,公比为2的等比数列
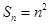
(2)证得
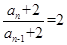 ,数列
,数列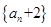 是以
是以 为首项,公比为2的等比数列
为首项,公比为2的等比数列试题分析:(1)当
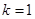 时,
时, ,则数列
,则数列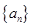 是以1为首项,公差为2的等差数列
是以1为首项,公差为2的等差数列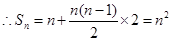
(2)当
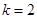 时,
时,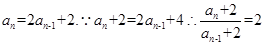
数列
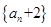 是以
是以 为首项,公比为2的等比数列
为首项,公比为2的等比数列点评:中档题,本题两道小题,均是首先明确k的取值,使数列的特征得以发现。数列的求和立足于“公式法”,应当注意到“分组求和法”“裂项相消法”“错位相减法”,均是高考考查的重要求和方法。

练习册系列答案
相关题目
 ___________ .
___________ .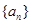 的前n项和为
的前n项和为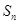 ,已知
,已知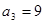 ,
, 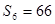 .
.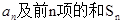 ;
;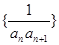 的前n项和为
的前n项和为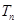 ,证明:
,证明: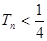 ;
;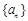 中,
中,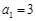 ,
,
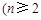 且
且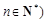 .
.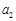 ,
,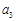 的值;
的值;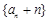 是等比数列,并求
是等比数列,并求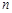 项和
项和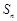 .
.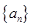 满足
满足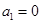 ,
,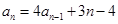
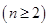 ,则通项
,则通项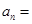 .
. }的前n项和Sn.
}的前n项和Sn.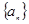 的前
的前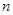 项和为
项和为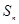 ,
,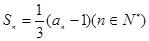
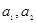 ;
;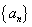 中,
中, 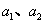 是正整数,且
是正整数,且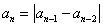 ,
,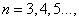 则称数列
则称数列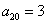 ,
,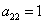 ,则
,则 .
.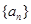 的前n项和为
的前n项和为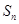 ,令
,令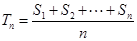 ,称
,称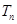 为数列
为数列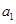 ,
,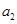 , ,
, ,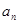 的“理想数”,已知数列
的“理想数”,已知数列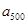 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2,