题目内容
 (2012•湖北模拟)如图,已知四棱锥P一ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
(2012•湖北模拟)如图,已知四棱锥P一ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=| 1 | 2 |
(1)求证AM=CM;
(2)N是PC的中点,求证DN∥平面AMC.
分析:(1)先证明BC⊥PC,利用在Rt△PAB中,M为PB的中点,则AM=
PB.在Rt△PBC中,M为PB的中点,则CM=
PB,得到AM=CM.
(2)连接DB交AC于F,取PM中点G,连接DG,FM,说明DG∥FM,证明DG∥平面AMC,连DN,GN,证明GN∥MC.然后证明DN∥平面ACM
| 1 |
| 2 |
| 1 |
| 2 |
(2)连接DB交AC于F,取PM中点G,连接DG,FM,说明DG∥FM,证明DG∥平面AMC,连DN,GN,证明GN∥MC.然后证明DN∥平面ACM
解答: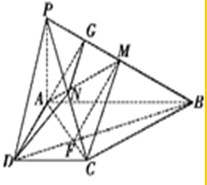 证明:(1)在直角梯形ABCD中,BC⊥AC,
证明:(1)在直角梯形ABCD中,BC⊥AC,
又∵PA⊥平面ABCD、BC?平面ABCD.
∴BC⊥PA,∴BC⊥平面PAC,
∴BC⊥PC,
在Rt△PAB中,M为PB的中点,则AM=
PB.
在Rt△PBC中,M为PB的中点,则CM=
PB,
∴AM=CM.
(2)连接DB交AC于F,
∵DC
AB,∴DF=
FB.
取PM中点G,连接DG,FM,则DG∥FM,
又DG?平面MAC,FM?平面AMC,
∴DG∥平面AMC,连DN,GN,则GN∥MC,
∴GN∥平面AMC,又GN∩DG=G,
∴平面DNG∥平面ACM,
又DN?平面DNG,
∴DN∥平面ACM.
 证明:(1)在直角梯形ABCD中,BC⊥AC,
证明:(1)在直角梯形ABCD中,BC⊥AC,又∵PA⊥平面ABCD、BC?平面ABCD.
∴BC⊥PA,∴BC⊥平面PAC,
∴BC⊥PC,
在Rt△PAB中,M为PB的中点,则AM=
| 1 |
| 2 |
在Rt△PBC中,M为PB的中点,则CM=
| 1 |
| 2 |
∴AM=CM.
(2)连接DB交AC于F,
∵DC
| ∥ |
. |
| 1 |
| 2 |
| 1 |
| 2 |
取PM中点G,连接DG,FM,则DG∥FM,
又DG?平面MAC,FM?平面AMC,
∴DG∥平面AMC,连DN,GN,则GN∥MC,
∴GN∥平面AMC,又GN∩DG=G,
∴平面DNG∥平面ACM,
又DN?平面DNG,
∴DN∥平面ACM.
点评:本题考查空间想象能力,逻辑推理能力,证明线段相等,直线与平面平行的判定定理的应用,是中档题.

练习册系列答案
相关题目
 (2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=
(2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=