Question

【题目】在平面内，定点A，B，C，O满足 |=2， = ，动点P，M满足 的最大值是（ ）
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：由 |=2知，O是△ABC的外心；

= ，

∴ ﹣ = ﹣ =0，

当 ﹣ =0时， = ，

即 = ，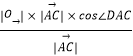

∴cos∠DAC=cos∠DAB

∴∠DAC=∠DAB，

∴O点在三角形的角A平分线上；

同理，O点在三角形的角B，角C平分线上；

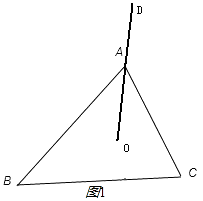
∴点定O的一定是△ABC的内心，如图1所示；

∴△ABC是正三角形，且边长为 =2 ；

如图2所示，建立平面直角坐标系；则B（0，0），C（2 ，0），A（ ，3）；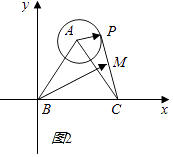

∵M满足| |=1，∴点P的轨迹方程为： +（y﹣3）2=1；

令x= +cosθ，y=3+sinθ，θ∈[0，2π），

由 = ，得M（ + cosθ， + sinθ），

∴| |2= + = +3sin（θ+ ）≤ ；

∴| |2的最大值是 ．

故选：B．