题目内容
【题目】数列{an}的前项和为Sn ， 且 
，用[x]表示不超过x的最大整数，如[﹣0.1]=﹣1，[1.6]=1，设bn=[an]，则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= ．
【答案】
﹣n﹣ 
【解析】解：由 
，①
可得a2﹣S1= 
，a2=a1+ = 
，
将n换为n﹣1，可得an﹣Sn﹣1= ，n≥2②
由an=Sn﹣Sn﹣1，
①﹣②可得，an+1=2an，
则an=a22n﹣2= 2n﹣2= 
2n，
上式对n=1也成立．
则an= 2n，
bn=[an]=[ 2n]，
当n=1时，b1+b2=0+1=1= 
﹣1﹣ ；
当n=2时，b1+b2+b3+b4=0+1+2+5=8= 
﹣2﹣ ；
当n=3时，b1+b2+b3+b4+b5+b6=0+1+2+5+10+21=39= 
﹣3﹣ ；
当n=4时，b1+b2+b3+b4+b5+b6+b7+b8=0+1+2+5+10+21+42+85=166= 
﹣4﹣ ；
则数列{bn}的前2n项和为b1+b2+b3+b4++b2n﹣1+b2n
= 
﹣n﹣ ．
另解：设T2n=b1+b2+b3+b4++b2n﹣1+b2n，
由T2n﹣T2n﹣2=22n﹣1﹣1，
累加可得数列{bn}的前2n项和为 
﹣n= ﹣n﹣ ．
所以答案是： ﹣n﹣ ．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系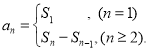
才能正确解答此题．
练习册系列答案
相关题目
