题目内容
一简单组合体的三视图如图(1)所示,则该组合体的体积为( )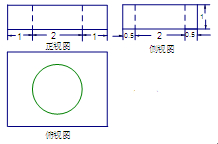
A.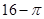 | B. | C.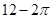 | D.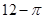 |
D
解析试题分析:由三视图可知,该几何体是在一个长方体中挖去一个圆柱而形成的,长方体的底面积为 ,高为
,高为 ,因此长方体的体积为
,因此长方体的体积为 ,圆柱的底面是一个直径为
,圆柱的底面是一个直径为 的圆,其半径长为
的圆,其半径长为 ,故其底面积为
,故其底面积为 ,高为
,高为 ,故圆柱的体积为
,故圆柱的体积为 ,综上所述,该几何体的体积为
,综上所述,该几何体的体积为 ,故选D.
,故选D.
考点:1.三视图;2.空间几何体的体积

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
设四面体的六条棱的长分别为1,1,1,1,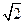 和
和 ,且长为
,且长为 的棱与长为
的棱与长为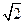 的棱异面,则
的棱异面,则 的取值范围是
的取值范围是
A.(0,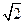 ) ) |
B.(0,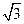 ) ) |
C.(1,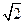 ) ) |
D.(1,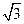 ) ) |
一个几何体的三视图如图所示,则该几何体的体积为( )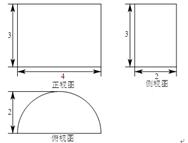
A.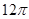 | B.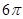 | C.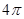 | D.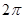 |
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
A. | B. | C. | D. |
将边长为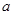 的正方形
的正方形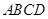 沿对角线
沿对角线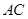 折起,使
折起,使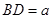 ,则三棱锥
,则三棱锥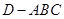 的体积为( )
的体积为( )
A.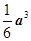 | B.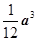 | C. | D.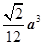 |
某空间几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |



 的棱长为
的棱长为 ,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )




 中,
中, 、
、 分别是棱
分别是棱 、
、 的中点,且
的中点,且 ,若侧棱
,若侧棱 ,则正三棱锥
,则正三棱锥


