题目内容
将边长为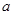 的正方形
的正方形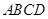 沿对角线
沿对角线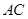 折起,使
折起,使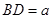 ,则三棱锥
,则三棱锥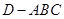 的体积为( )
的体积为( )
A.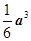 | B.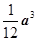 | C. | D.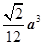 |
D
解析试题分析:
 是
是 中点,连接
中点,连接
 都是等腰直角三角形
都是等腰直角三角形  ,
, 也是等腰直角三角形
也是等腰直角三角形 ,
, 平面
平面 ,
, 就是三棱锥
就是三棱锥 的高
的高 三棱锥
三棱锥 的体积:
的体积: ,故选D.
,故选D.
考点:1.翻折图形;2.线面垂直的判定,性质;3.体积公式.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
平面 截球O的球面所得圆的半径为1,球心O到平面α的距离为
截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,则此球的体积为( )
,则此球的体积为( )
A. π π | B.4 π π | C.4 π π | D.6 π π |
一简单组合体的三视图如图(1)所示,则该组合体的体积为( )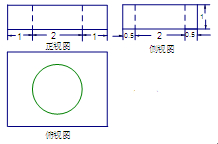
A.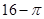 | B. | C.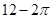 | D.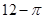 |
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )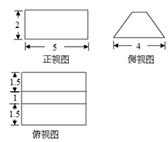
A.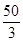  | B.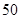  | C.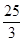  | D.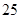  |
某几何体的三视图如图所示,则该几何体的体积为( )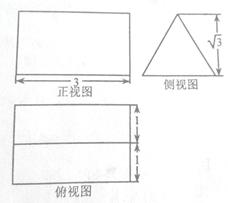
| A.6 | B.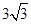 | C.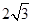 | D.3 |
已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1,直径为4的球的体积为V2,则( )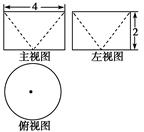
| A.1∶2 | B.2∶1 | C.1∶1 | D.1∶4 |
 的侧棱长和底面边长均为
的侧棱长和底面边长均为 ,且侧棱
,且侧棱 底面
底面 ,其正视图是边长为
,其正视图是边长为









