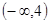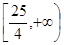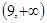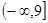题目内容
(本题满分14分) 已知 是方程
是方程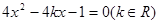 的两个不等实根,函数
的两个不等实根,函数 的定义域为
的定义域为 .
.
⑴当 时,求函数
时,求函数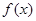 的值域;
的值域;
⑵证明:函数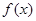 在其定义域
在其定义域 上是增函数;
上是增函数;
⑶在(1)的条件下,设函数 ,
,
若对任意的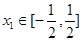 ,总存在
,总存在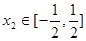 ,使得
,使得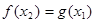 成立,
成立,
求实数 的取值范围.
的取值范围.
 是方程
是方程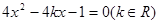 的两个不等实根,函数
的两个不等实根,函数 的定义域为
的定义域为 .
.⑴当
 时,求函数
时,求函数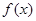 的值域;
的值域;⑵证明:函数
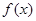 在其定义域
在其定义域 上是增函数;
上是增函数;⑶在(1)的条件下,设函数
 ,
, 若对任意的
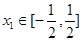 ,总存在
,总存在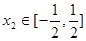 ,使得
,使得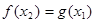 成立,
成立,求实数
 的取值范围.
的取值范围.⑴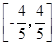 ;⑵只需证
;⑵只需证 >0.⑶
>0.⑶ 。
。
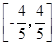 ;⑵只需证
;⑵只需证 >0.⑶
>0.⑶ 。
。试题分析:(1)
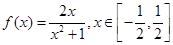
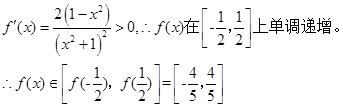 ……………4分
……………4分(2)

∵
 是方程
是方程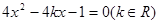 的两个不等实根
的两个不等实根即是方程
 (抛物线开口向下,两根之内的函数值必为正值)
(抛物线开口向下,两根之内的函数值必为正值)∵当
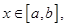
 ……………7分
……………7分∴
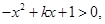
∴
 >0.
>0.∴函数
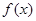 在其定义域
在其定义域 上是增函数……………9分
上是增函数……………9分(3)由题意知:g(x)的值域是f(x)值域的子集。
由(1)知,f(x)的值域是
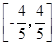 ,
,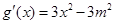 ,
,
| x | 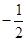 | 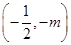 | -m | 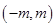 | m | 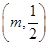 |  |
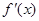 | | + | 0 | - | 0 | + | |
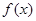 | 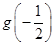 | 递增 | 极大值g(-m) | 递减 | 极小值g(m) | 递增 | 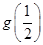 |
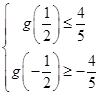 ,
,∴欲使g(x)的值域是f(x)值域的子集
只需
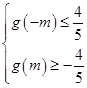
解得:
 ……………14分
……………14分点评:做本题的关键是分析出“在(1)的条件下,设函数
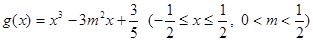 , 若对任意的
, 若对任意的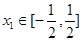 ,总存在
,总存在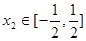 ,使得
,使得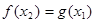 成立”的含义,其含义为“(x)的值域是f(x)值域的子集”。
成立”的含义,其含义为“(x)的值域是f(x)值域的子集”。
练习册系列答案
相关题目
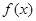 为定义在
为定义在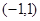 上的奇函数,当
上的奇函数,当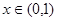 时,
时,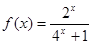 ;
;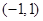 上的解析式;
上的解析式;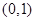 上的单调性,并给出证明.
上的单调性,并给出证明.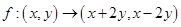 ,在映射
,在映射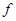 下
下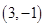 的原象是( )
的原象是( ) 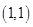
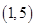
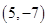

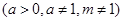 是奇函数.
是奇函数.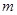 的值;
的值;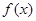 在
在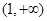 上的单调性,并给出证明;
上的单调性,并给出证明;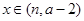 时,函数
时,函数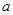 与
与 的值。
的值。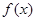 =
=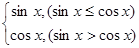 ,给出下列四个命题:①该函数是以
,给出下列四个命题:①该函数是以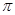 为最小正周期的周期函数;②当且仅当
为最小正周期的周期函数;②当且仅当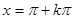 (k∈Z)时,该函数取得最小值-1;
(k∈Z)时,该函数取得最小值-1;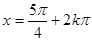 (k∈Z)对称;
(k∈Z)对称;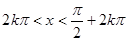 (k∈Z)时,0<
(k∈Z)时,0<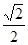 .
. .
.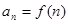 ,写出数列
,写出数列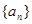 的前5项;
的前5项;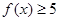 .
.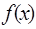 为奇函数,且在
为奇函数,且在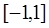 上为增函数,
上为增函数,  , 若
, 若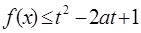 对所有
对所有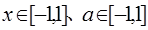 都成立,求
都成立,求 的取值范围。
的取值范围。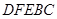 内修建一个矩形
内修建一个矩形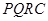 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且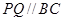 ,
,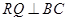 ,另外
,另外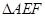 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量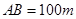 ,
,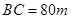 ,
, 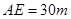 ,
,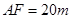 .
.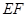 的方程;
的方程;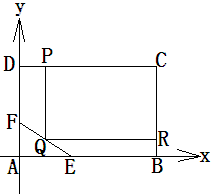
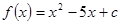 ,
,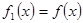 ,
,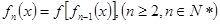 ,
,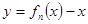 不存在零点,则
不存在零点,则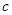 的范围是 ( )
的范围是 ( )