题目内容
若函数f（x）=logax（a＞0，a≠1）满足f（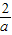
）
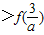，则f（1-
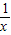）＞1的解集是（ ）A．0
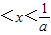
B．0
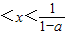
C．1
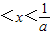
D．1
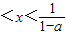
【答案】分析：先由条件f（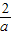
）
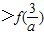，得到loga 
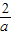＞loga 
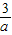从而求出a的取值范围，利用对数函数的单调性与特殊点化简不等式f（1-
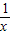）＞1为整式不等式即可求解．
解答：解：∵满足f（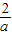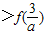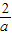
）
，
∴loga
＞loga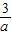 
⇒loga2＞loga3⇒0＜a＜1，
则f（1-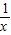
）＞1?loga（1-
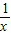）＞log a1⇒0＜1-
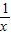＜a⇒1＜x＜
．
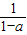故选D．
点评：本小题主要考查函数单调性的应用、对数函数的单调性与特殊点、不等式的解法等基础知识，考查运算求解能力与转化思想．属于基础题．
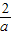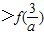），得到l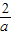oga ＞loga 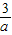从而求出a的取值范围，利用对数函数的单调性与特殊点化简不等式f（1-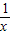）＞1为整式不等式即可求解．解答：解：∵满足f（
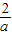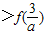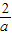），∴loga
＞loga 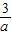⇒loga2＞loga3⇒0＜a＜1，则f（1-
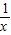）＞1?loga（1-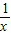）＞log a1⇒0＜1-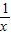＜a⇒1＜x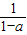＜．故选D．
点评：本小题主要考查函数单调性的应用、对数函数的单调性与特殊点、不等式的解法等基础知识，考查运算求解能力与转化思想．属于基础题．
练习册系列答案
快捷英语周周练系列答案
相关题目
的定义域为M，g(x)＝lo
(2＋x＝6x2)的单调递减区间是开区间N，设全集U＝R，则M∩CU(N)＝________．
(x2－2ax＋3)．
(m∈R)
[8－f(x)]在[1，＋∞)上是单调减函数，求实数m的取值范围；
上的最大值．
的奇函数，a为常数，
)x＋m恒成立，求实数m的取值范围．