题目内容
已知![]() 、
、![]() 、
、![]() 是同一平面内三条不重合自上而下的平行直线.
是同一平面内三条不重合自上而下的平行直线.
(Ⅰ)如果![]() 与
与![]() 间的距离是1,
间的距离是1,![]() 与
与![]() 间的距离也是1,可以把一个正三角形
间的距离也是1,可以把一个正三角形![]() 的三顶点分别放在
的三顶点分别放在![]() ,
,![]() ,
,![]() 上,求这个正三角形
上,求这个正三角形![]() 的边长;
的边长;
(Ⅱ)如图,如果![]() 与
与![]() 间的距离是1,
间的距离是1,![]() 与
与![]() 间的距离是2,能否把一个正三角形
间的距离是2,能否把一个正三角形![]() 的三顶点分别放在
的三顶点分别放在![]() ,
,![]() ,
,![]() 上,如果能放,求
上,如果能放,求![]() 和
和![]() 夹角的正切值并求该正三角形边长;如果不能,说明为什么?
夹角的正切值并求该正三角形边长;如果不能,说明为什么?
(Ⅲ)如果边长为2的正三角形![]() 的三顶点分别在
的三顶点分别在![]() ,
,![]() ,
,![]() 上,设
上,设![]() 与
与![]() 的距离为
的距离为![]() ,
,![]() 与
与![]() 的距离为
的距离为![]() ,求
,求![]() 的范围?
的范围?

略
解析:
(Ⅰ)∵![]() 到直线
到直线![]() 的距离相等,
的距离相等,
∴![]() 过
过![]() 的中点
的中点![]() , 1分
, 1分
∴![]() 2分
2分
∴边长![]() ……………3分
……………3分
(Ⅱ)设边长为![]()
![]() 与
与![]() 的夹角为
的夹角为![]() ,由对称性,不妨设
,由对称性,不妨设![]() ,
,
∴![]()
![]() 5分
5分
两式相比得:
![]()
![]()
∴![]() ………………7分
………………7分
∴![]()
∴![]() 边长
边长 ………………8分
………………8分
(Ⅲ)![]()
![]()
![]()
=![]()
=![]() ……………………………10分
……………………………10分
∵![]() ,∴
,∴![]()
∴![]() ,
,
∴![]() ……………12分.
……………12分.

 阅读快车系列答案
阅读快车系列答案 ,
, ,
,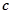 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中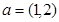 .
.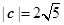 ,且
,且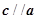 ,求
,求 ,且
,且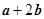 与
与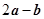 垂直,求
垂直,求 .
.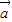 ,
,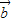 ,
,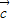 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中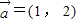 .
.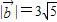 ,且
,且 ,求
,求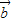 的坐标;
的坐标;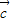 与
与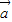 的夹角θ的余弦值为
的夹角θ的余弦值为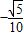 ,且
,且 ,求
,求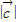 .
.