Question

如图,在四棱锥S—ABCD中,底面ABCD是正方形,SA⊥底面ABCD, SA=AB,点M是SD的中点,AN⊥SC,且交SC于点N.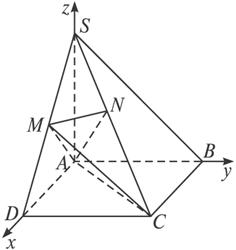

(1)求证:SB∥平面ACM;

(2)求二面角D-A-C-M的大小;

(3)求证:平面SAC⊥平面AMN.

Answer 1

(1)证明:连结BD交AC于E,连结ME.

∵ABCD是正方形,∴E是BD的中点.∵M是SD的中点,∴ME是△DSB的中位线.∴ME∥SB.

又∵ME平面ACM,SB平面ACM,

∴SB∥平面ACM.

解法一:(2)解:取AD中点F,则MF∥SA.作FQ⊥AC于Q,连结MQ.

∵SA⊥底面ABCD,∴MF⊥底面ABCD.∴FQ为MQ在平面ABCD内的射影.∵PQ⊥AC,∴MQ⊥AC.

∴∠FQM为二面角DACM的平面角.

设SA=AB=a,在Rt△MFQ中,MF=SA=,FQ=DE=a,∴tan∠FQM==.

∴二面角DACM的大小为arctan.

(3)证明:由条件有DC⊥SA,DC⊥DA,∴DC⊥平面SAD.∴AM⊥DC.

又∵SA=AD,M是SD的中点,∴AM⊥SD.∴AM⊥平面SDC.

∴SC⊥AM.由已知SC⊥AN,∴SC⊥平面AMN.

又SC平面SAC,∴平面SAC⊥平面AMN.

解法二:(2)解:如图,以A为坐标原点,建立空间直角坐标系A—xyz,

由SA=AB,故设AB=AD=AS=1,则A(0,0,0),B(0,1,0),C(1,1,0),D(1,0,0),S(0,0,1),M(,0,).

∵SA⊥底面ABCD,

∴是平面ABCD的法向量,=(0,0,1).

设平面ACM的法向量为n=(x,y,z),

=(1,1,0),=(,0,),

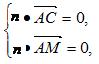则即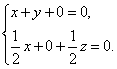

∴

令x=1,则n=(1,-1,-1).

∴cos〈,n〉=

∴二面角D-AC-M的大小为arccos.

(3)证明:∵=(,0,),=(-1,-1,1),

∴·=+=0.

∴⊥.

又∵SC⊥AN且AN∩AM=A,∴SC⊥平面AMN.又SC平面SAC,

∴平面SAC⊥平面AMN.