题目内容
设锐角三角形ABC的内角A、B、C的对边分别为a、b、c，a＝2bsin A.
(1)求B的大小．
(2)若a＝3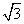
，c＝5，求b.
解 (1)∵a＝2bsin A，∴sin A＝2sin B·sin A，
∴sin B＝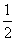
.∵0<B<
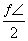，∴B＝30°.
(2)∵a＝3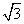，c＝5，B＝30°.
由余弦定理b2＝a2＋c2－2accos B
＝(3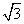)2＋52－2×3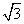×5×cos 30°＝7.
∴b＝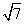
.
练习册系列答案
相关题目
题目内容
设锐角三角形ABC的内角A、B、C的对边分别为a、b、c，a＝2bsin A.
(1)求B的大小．
(2)若a＝3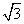，c＝5，求b.
解 (1)∵a＝2bsin A，∴sin A＝2sin B·sin A，
∴sin B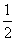＝.∵0<B<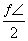，∴B＝30°.
(2)∵a＝3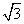，c＝5，B＝30°.
由余弦定理b2＝a2＋c2－2accos B
＝(3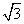)2＋52－2×3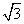×5×cos 30°＝7.
∴b＝.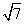
≥a恒成立，则实数a的取值范围是( )
ac，则角B的值为( )
B.
＝
，则B＝________.
,
,
,则
等于 ( )
B．
C．
D．
的图象沿x轴方向左平移
个单位，平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是（ ）
B．
D．
到直线
的距离是（ ）
Ｂ．
C．
D．
满足
则
的最大值为（ ）
B.
C.
D. 