题目内容
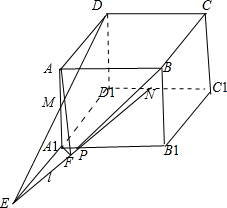
 在棱长为a的正方体ABCD-A1B1C1D1中,M、N分别为A1A、D1C1的中点,过D、M、N三点的平面与正方体的下底面A1B1C1D1相交与直线l.
在棱长为a的正方体ABCD-A1B1C1D1中,M、N分别为A1A、D1C1的中点,过D、M、N三点的平面与正方体的下底面A1B1C1D1相交与直线l.(1)画出直线l的位置;
(2)设l∩A1B1=P,求PB的长;
(3)求A到l的距离.
考点:点、线、面间的距离计算,平行公理
专题:空间位置关系与距离
分析:(1)连接DM并延长交D1A1延长线于E,连接NE即是所求直线l;
(2)容易求得A1P=
a,所以B1P=
a,又BB1=a,所以在Rt△BB1P中,可求出BP;
(3)求A到l的距离,所以想着找过a,与l垂直的线段,所以过A1作l的垂线,垂足为F,连接AF,容易说明AF⊥l,所以根据一些边的长度求AF长度即可.
(2)容易求得A1P=
| 1 |
| 4 |
| 3 |
| 4 |
(3)求A到l的距离,所以想着找过a,与l垂直的线段,所以过A1作l的垂线,垂足为F,连接AF,容易说明AF⊥l,所以根据一些边的长度求AF长度即可.
解答:
解:(1)如图,连接DM,并延长交DA1延长线于E,连接NE,则NE即为所找直线l;
 (2)根据已知条件知:MA1∥DD1,且MA1=
(2)根据已知条件知:MA1∥DD1,且MA1=
DD1,∴A1为ED1的中点;
A1P=
D1N=
a,∴B1P=
a,BB1=a,∴PB=
=
;
(3)过A1作A1F⊥l,垂足为F,连接AF,∵AA1⊥平面ED1N,EN?平面ED1N,∴AA1⊥EN即EN⊥AA1,又EN⊥A1F,AA1∩A1F=A1,∴EN⊥平面AA1F,AF?平面AA1F,∴EN⊥AF,∴求A到l的距离,求AF的长度即可;
EP=
EN=
=
,∴在Rt△EA1P中,A1E•A1P=EP•A1F,∴a•
=
•A1F,∴A1F=
;
∴在Rt△AA1P中,AA1,AP=
=
,即A到l的距离为:
.
 (2)根据已知条件知:MA1∥DD1,且MA1=
(2)根据已知条件知:MA1∥DD1,且MA1=| 1 |
| 2 |
A1P=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
|
| 5a |
| 4 |
(3)过A1作A1F⊥l,垂足为F,连接AF,∵AA1⊥平面ED1N,EN?平面ED1N,∴AA1⊥EN即EN⊥AA1,又EN⊥A1F,AA1∩A1F=A1,∴EN⊥平面AA1F,AF?平面AA1F,∴EN⊥AF,∴求A到l的距离,求AF的长度即可;
EP=
| 1 |
| 2 |
| 1 |
| 2 |
4a2+
|
| ||
| 4 |
| a |
| 4 |
| ||
| 4 |
| a | ||
|
∴在Rt△AA1P中,AA1,AP=
a2+
|
3
| ||
| 17 |
3
| ||
| 17 |
点评:三角形的中位线,直角三角形中边的关系,线面垂直的性质,线面垂直的判定定理.

练习册系列答案
相关题目
下表显示出函数值y随自变量x变化的一组数据,由此判断符合这组数据的最恰当的函数模型是( )
| x | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
| y | … | 13 | 15 | 17 | 19 | 21 | 23 | 25 | … |
| A、一次函数模型 |
| B、二次函数模型 |
| C、指数函数模型 |
| D、对数函数模型 |