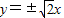题目内容
 如图双曲线
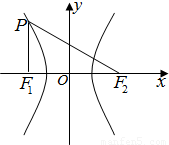
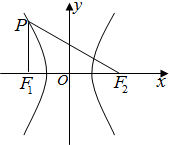
如图双曲线 焦点F1,F2,过点F1作垂直于x轴的直线交双曲线于P点,且∠PF2F1=30°,则双曲线的渐近线是
焦点F1,F2,过点F1作垂直于x轴的直线交双曲线于P点,且∠PF2F1=30°,则双曲线的渐近线是
- A.y=±x
- B.y=±2x
- C.

- D.y=±4x
C
分析:先根据焦点三角形PF2F1中角的大小求出三边之间的关系,在根据双曲线定义把三边用含a,c的式子表示,就可得到含a,c的关系式,把c用a,b表示,求出a,b的关系式,再代入双曲线的渐近线方程即可.
解答:∵PF1⊥F1F2,∠PF2F1=30°
∴在Rt△PF2F1中,|PF2|= ,,|PF1|=
,,|PF1|=
∵P点在双曲线 上,
上,
∴|PF2|-|PF1|=2a,|F2F1|=2c
∴ -
- =2a
=2a
即
∴ ,
,
∵c2=a2+b2,∴a2+b2=3a2
∴b2=2a2,b= a
a
∵双曲线 焦点在x轴上,
焦点在x轴上,
∴渐近线方程为y=± =±
=± =±
=± x
x
∴渐近线方程为y=± x
x
故选C
点评:本题考查了焦点三角形中三边关系,以及双曲线的渐近线的求法,属于圆锥曲线中的常规题.
分析:先根据焦点三角形PF2F1中角的大小求出三边之间的关系,在根据双曲线定义把三边用含a,c的式子表示,就可得到含a,c的关系式,把c用a,b表示,求出a,b的关系式,再代入双曲线的渐近线方程即可.
解答:∵PF1⊥F1F2,∠PF2F1=30°
∴在Rt△PF2F1中,|PF2|=
 ,,|PF1|=
,,|PF1|=
∵P点在双曲线
 上,
上,∴|PF2|-|PF1|=2a,|F2F1|=2c
∴
 -
- =2a
=2a即

∴
 ,
,
∵c2=a2+b2,∴a2+b2=3a2
∴b2=2a2,b=
 a
a∵双曲线
 焦点在x轴上,
焦点在x轴上,∴渐近线方程为y=±
 =±
=± =±
=± x
x∴渐近线方程为y=±
 x
x故选C
点评:本题考查了焦点三角形中三边关系,以及双曲线的渐近线的求法,属于圆锥曲线中的常规题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
 如图双曲线
如图双曲线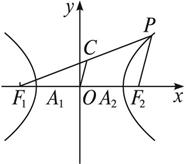
 焦点F1,F2,过点F1作垂直于x轴的直线交双曲线于P点,且∠PF2F1=30°,则双曲线的渐近线是( )
焦点F1,F2,过点F1作垂直于x轴的直线交双曲线于P点,且∠PF2F1=30°,则双曲线的渐近线是( )