题目内容
 如图双曲线
如图双曲线| x2 |
| a2 |
| y2 |
| b2 |
分析:先根据焦点三角形PF2F1中角的大小求出三边之间的关系,在根据双曲线定义把三边用含a,c的式子表示,就可得到含a,c的关系式,把c用a,b表示,求出a,b的关系式,再代入双曲线的渐近线方程即可.
解答:解:∵PF1⊥F1F2,∠PF2F1=30°
∴在Rt△PF2F1中,|PF2|=
,,|PF1|=
∵P点在双曲线
-
=1上,
∴|PF2|-|PF1|=2a,|F2F1|=2c
∴
-
=2a
即
-
=2a
∴
=2c,
=a2
∵c2=a2+b2,∴a2+b2=3a2
∴b2=2a2,b=
a
∵双曲线
-
=1焦点在x轴上,
∴渐近线方程为y=±
x=±
x=±
x
∴渐近线方程为y=±
x
故选C
∴在Rt△PF2F1中,|PF2|=
| 2|F1F2| | ||
|
| |F1F2| | ||
|
∵P点在双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴|PF2|-|PF1|=2a,|F2F1|=2c
∴
| 2|F1F2| | ||
|
| |F1F2| | ||
|
即
| 2×2c | ||
|
| 2c | ||
|
∴
| 2c | ||
|
| c2 |
| 3 |
∵c2=a2+b2,∴a2+b2=3a2
∴b2=2a2,b=
| 2 |
∵双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴渐近线方程为y=±
| b |
| a |
| ||
| a |
| 2 |
∴渐近线方程为y=±
| 2 |
故选C
点评:本题考查了焦点三角形中三边关系,以及双曲线的渐近线的求法,属于圆锥曲线中的常规题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
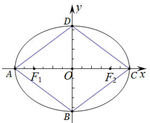 如图椭圆
如图椭圆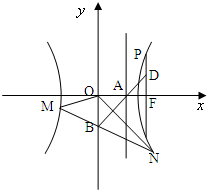 (2008•湖北模拟)如图,已知双曲线
(2008•湖北模拟)如图,已知双曲线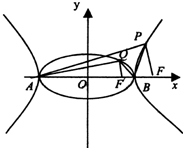 如图,F′,F分别为椭圆
如图,F′,F分别为椭圆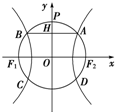 如图,双曲线
如图,双曲线