题目内容
如图5所示,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,点
,点 在线段
在线段 上,
上, 平面
平面 .
.
(1)证明: 平面
平面 ;
;
(2)若 ,
, ,求二面角
,求二面角 的正切值.
的正切值.

 解:
解:
(1)因为 平面
平面 ,
, 平面
平面 ,所以
,所以 .又因为
.又因为 平面
平面 ,
, 平面
平面 ,所以
,所以 .而
.而 ,
, 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 . ---------5分
. ---------5分
(2)由(1)可知 平面
平面 ,而
,而 平面
平面 ,所以
,所以 ,而
,而 为矩形,
为矩形,
所以 为正方形,于是
为正方形,于是 .
.
以 点为原点,
点为原点, 、
、 、
、 为
为 轴、
轴、 轴、
轴、 轴,建立空间直角坐标系
轴,建立空间直角坐标系 .则
.则
 、
、 、
、 、
、 ,于是
,于是 ,
, .
.
设平面 的一个法向量为
的一个法向量为
 ,则
,则 ,从而
,从而 ,
,
令 ,得
,得 .而平面
.而平面 的一个法向量为
的一个法向量为
 .
.
所以二面角 的余弦值为
的余弦值为 ,
,
于是二面角 的正切值为3. ----------12分
的正切值为3. ----------12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
,
 ,
, ,…,
,…, 中最大的是()
中最大的是() C.
C.  D.
D.  满足
满足 ,且a5·a6=2,则log2a1+ log2a2+…+ log2a10=( )A.2 B.4 C.5 D.25
,且a5·a6=2,则log2a1+ log2a2+…+ log2a10=( )A.2 B.4 C.5 D.25 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点, 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为
的离心率为 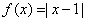
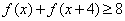 ;
;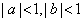 ,且
,且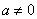 ,求证:
,求证: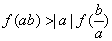 .
. 的展开式的各项系数之和为
的展开式的各项系数之和为 ,二项式系数之和为
,二项式系数之和为 ,若
,若 ,则展开式中常数项为( )
,则展开式中常数项为( )  的值域是 ( )
的值域是 ( ) B.
B.  C.
C.  D.
D. 
 ,且
,且 ,则
,则 .
.