题目内容
已知F1、F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,点P为双曲线上任意一点,过F1作∠F1PF2的平分线的垂线,垂足为Q,则点Q的轨迹方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A.x2+y2=a2 | B.x2+y2=b2 | C.x2-y2=a2 | D.x2-y2=b2 |
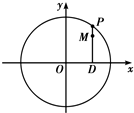
点F1关于∠F1PF2的角平分线PQ的对称点M在直线PF2的延长线上,
故|F2M|=|PF1|-|PF2|=2a,
又OQ是△F2F1M的中位线,
故|OQ|=a,
点Q的轨迹是以原点为圆心,a为半径的圆,
则点Q的轨迹方程为x2+y2=a2
故选A.
故|F2M|=|PF1|-|PF2|=2a,
又OQ是△F2F1M的中位线,
故|OQ|=a,
点Q的轨迹是以原点为圆心,a为半径的圆,
则点Q的轨迹方程为x2+y2=a2
故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
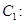
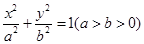 的离心率为
的离心率为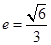 ,过
,过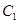 的左焦点
的左焦点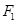 的直线
的直线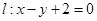 被圆
被圆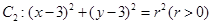 截得的弦长为
截得的弦长为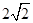 .
.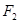 ,在圆
,在圆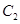 上是否存在点
上是否存在点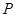 ,满足
,满足 ,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.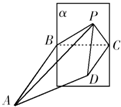
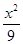 +
+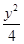 =1的交点个数是( )
=1的交点个数是( )