题目内容
20.在△ABC中,角A,B,C的对边分别为a,b,c,且满足bcosA=(2c+a)cos(A+C).(Ⅰ)求角B的大小;
(Ⅱ)求函数f(x)=2sin2x+sin(2x-B)(x∈R)的最大值.
分析 (Ⅰ)由正弦定理和和差角的三角函数公式可得cosB,可得角B;
(Ⅱ)由(Ⅰ)和三角函数公式化简可得f(x)=$\sqrt{3}$sin(2x-$\frac{π}{6}$),易得函数最大值.
解答 解:(Ⅰ)∵在△ABC中bcosA=(2c+a)cos(A+C),
∴由正弦定理可得sinBcosA=(2sinC+sinA)(-cosB),
∴sinBcosA+cosBsinA=-2sinCcosB,
∴sin(A+B)=-2sinCcosB,即sinC=-2sinCcosB,
约掉sinC可得cosB=-$\frac{1}{2}$,B=$\frac{2π}{3}$;
(Ⅱ)由(Ⅰ)化简可得f(x)=2sin2x+sin(2x-$\frac{2π}{3}$)
=2sin2x+sin2xcos$\frac{2π}{3}$-cos2xsin$\frac{2π}{3}$
=2sin2x-$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x
=$\frac{3}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x=$\sqrt{3}$sin(2x-$\frac{π}{6}$),
∴当2x-$\frac{π}{6}$=2kπ+$\frac{π}{2}$即x=kπ+$\frac{π}{3}$,k∈Z时,函数取最大值$\sqrt{3}$.
点评 本题考查正余弦定理解三角形,涉及和差角的三角函数公式和三角函数的最值,属中档题.

练习册系列答案
相关题目
8.已知向量$\overrightarrow{a}$=(2x+1,3),$\overrightarrow{b}$=(2-x.1),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x的值等于( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | 1 | D. | -1 |
15.设等比数列{an}的前n项和为Sn,若a2=3,且a2015+a2016=0,则S101等于( )
| A. | 3 | B. | 303 | C. | -3 | D. | -303 |
5.已知m,n表示两条不同直线,α,β,γ表示三个不同平面,以下命题正确的是( )
| A. | 若m∥α,m∥β,则α∥β | B. | 若m?α,n?α,m∥β,n∥β,则α∥β | ||
| C. | 若m∥α,n?α,则m∥n | D. | 若α∥β,γ∩α=m,γ∩β=n,则 m∥n |
12.某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(x个月)和市场占有率(y%)的几组相关对应数据;
(1)根据上表中的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过0.5%(精确到月)
附:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过0.5%(精确到月)
附:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
9.阅读如图的程序框图,当该程序运行后输出的S值是( )
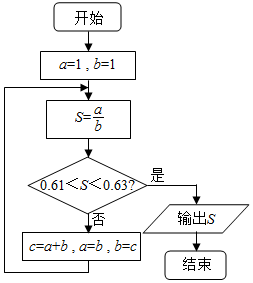

| A. | $\frac{3}{5}$ | B. | $\frac{5}{8}$ | C. | $\frac{8}{13}$ | D. | $\frac{13}{21}$ |
10.下列命题中是全称命题,并且又是真命题的是( )
| A. | 所有菱形的四条边都相等 | B. | ?x0∈N,使2x0为偶数 | ||
| C. | 对?x∈R,x2+2x+1>0 | D. | π是无理数 |
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC∩BD=O,A1O⊥底面ABCD,AB=AA1=2.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,AC∩BD=O,A1O⊥底面ABCD,AB=AA1=2.