题目内容
若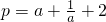 (a>0),q=arccost(-1≤t≤1),则下列不等式恒成立的是
(a>0),q=arccost(-1≤t≤1),则下列不等式恒成立的是
- A.p≥π>q
- B.p>q≥0
- C.4>p≥q
- D.p≥q>0
B
分析:先由基本不等式确定p的范围,再由arccost的值域确定q的范围即可得到答案.
解答:∵ 当a=1时等号成立
当a=1时等号成立
q=arccost∈[0,π]
∴p>q≥0
故选B.
点评:本题主要考查通过运用基本不等式来比较大小.
分析:先由基本不等式确定p的范围,再由arccost的值域确定q的范围即可得到答案.
解答:∵
 当a=1时等号成立
当a=1时等号成立q=arccost∈[0,π]
∴p>q≥0
故选B.
点评:本题主要考查通过运用基本不等式来比较大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=ax(a>0,a≠1),g(x)=-x2+2x+2,设函数F(x)=min{f(x),g(x)},(min{p,q}表示p,q中的较小值),若F(x)<2恒成立,则a的取值范围是( )
| A、(1,2) | ||
| B、(0,1)或(1,2) | ||
C、(1,
| ||
D、(0,1)或(1,
|