题目内容
已知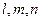 是三条不重合的直线,
是三条不重合的直线,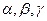 是三个不重合的平面,给出下列四个命题:
是三个不重合的平面,给出下列四个命题:
①若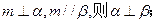
②若直线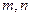 与平面
与平面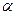 所成的角相等,则
所成的角相等,则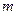 //
//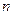 ;
;
③存在异面直线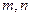 ,使得
,使得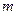 //
//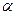 ,
,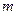 //
//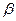 ,
,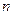 //
//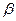 ,则
,则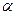 //
//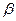 ;
;
④若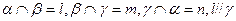 ,则
,则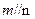 ;
;
其中正确命题的个数是
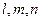 是三条不重合的直线,
是三条不重合的直线,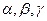 是三个不重合的平面,给出下列四个命题:
是三个不重合的平面,给出下列四个命题:①若
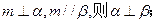
②若直线
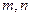 与平面
与平面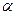 所成的角相等,则
所成的角相等,则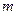 //
//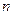 ;
;③存在异面直线
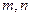 ,使得
,使得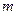 //
//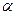 ,
,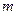 //
//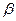 ,
,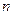 //
//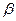 ,则
,则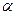 //
//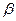 ;
;④若
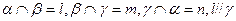 ,则
,则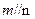 ;
;其中正确命题的个数是
| A.1 | B.2 | C.3 | D.4 |
C
略

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
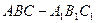 ,底面三角形
,底面三角形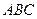 为正三角形,侧棱
为正三角形,侧棱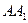
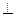 底面
底面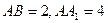 ,
,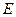 为
为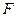 为
为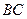 中点.
中点.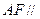 平面
平面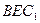 ;
;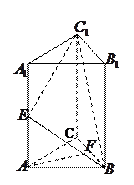
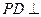 平面
平面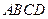 ,
,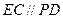 ,
,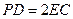 ,
, 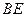 //平面
//平面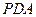 ;
;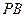 的中点,求证:
的中点,求证: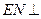 平面
平面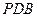 ;
;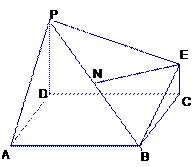
 ,∠PAB=60°。
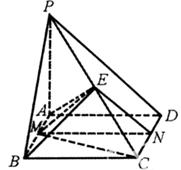
,∠PAB=60°。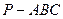 中,
中,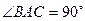 ,
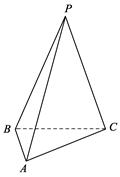
,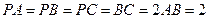 ,
,
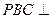 面
面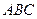
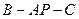 的余弦值.
的余弦值.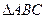 中,
中,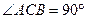 ,
,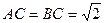 ,
,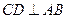 ,
,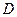 为垂足.沿
为垂足.沿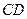 将
将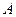 、
、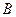 ,使得
,使得 .
.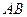 上是否存在点
上是否存在点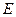 ,使
,使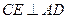 ?若存在,求出
?若存在,求出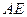 的长;若不存在,说明理由;
的长;若不存在,说明理由; 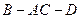 的平面角的正切值.
的平面角的正切值.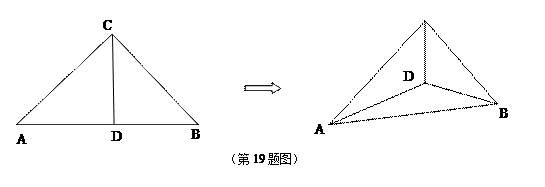
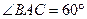 ,D为BC的中点。
,D为BC的中点。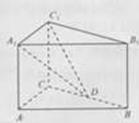
 1—C的大小。
1—C的大小。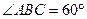 ,点M
,点M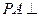 平面ABCD,AC、BD交于点O。
平面ABCD,AC、BD交于点O。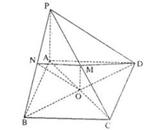
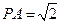 ,求证:AM
,求证:AM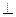 平面PBD;
平面PBD;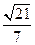 ,求PA的长
,求PA的长