题目内容
对实数m,直线(m+2)x-(2m-1)y-(3m+| 39 |
| 2 |
| x2 |
| 9 |
| y2 |
| m |
分析:由椭圆方程可得m>0且m≠9,令y=0求出直线与x轴的交点坐标,根据椭圆与x轴的交点坐标为(3,0)和(-3,0)可列出关于m的不等式,求出m的解集即可.
解答:解:根据题意知m>0且m≠9,然后令y=0,解得直线与x轴的交点坐标为(
,0)
而椭圆与x轴的交点为(3,0)和(-3,0),所以直线与圆横有公共点即可得到-3≤
≤3,解得m≥
所以m的取值范围是[
,9)∪(9,+∞)
故答案为:[
,9)∪(9,+∞)
3m+
| ||
| m+2 |
而椭圆与x轴的交点为(3,0)和(-3,0),所以直线与圆横有公共点即可得到-3≤
3m+
| ||
| m+2 |
| 9 |
| 2 |
所以m的取值范围是[
| 9 |
| 2 |
故答案为:[
| 9 |
| 2 |
点评:此题学生容易忽视m≠9的情况,是一道易错题.要求学生掌握直线与椭圆恒有交点的条件.

练习册系列答案
相关题目
 )=0和椭圆
)=0和椭圆 恒有公共点,则m的取值范围是 ________.
恒有公共点,则m的取值范围是 ________.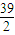 )=0和椭圆
)=0和椭圆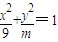 恒有公共点,则m的取值范围是 .
恒有公共点,则m的取值范围是 .