题目内容
已知F1、F2是两定点，|
|=2a（a＞0），动点P与F1、F2在同一平面内，且满足|
+
|=4a，则动点P的轨迹是（ ）
| F1F2 |
| PF1 |
| PF2 |
| A、椭圆 | B、圆 | C、直线 | D、线段 |
分析：以F1F2所在的直线为x轴，其垂直平分线为y轴，建立坐标系．讨论点P在x轴上与不在x 轴上两种情况得
+
=2
，又因为|
+
|=4a所以有|OP|=2a．再根据圆的定义得到动点P的轨迹是圆．
| PF1 |
| PF2 |
| PO |
| PF1 |
| PF2 |
解答：
解：以F1F2所在的直线为x轴，其垂直平分线为y轴，建立直角坐标系．如图所示
当P点不在x 轴上时
在△PF1F2中，
+
=2
又∵
+
= 4a
∴|
|=2a
∴|OP|=2a
当P点在x轴上时
∵|
|=2a且|
+
|=4a
∴经检验知也满足|OP|=2a
由以上得|OP|=2a
∴点p是在以O为圆心，以2a为半径的圆上．
∴动点P的轨迹是圆．
故选B．
解：以F1F2所在的直线为x轴，其垂直平分线为y轴，建立直角坐标系．如图所示当P点不在x 轴上时
在△PF1F2中，
| PF1 |
| PF2 |
| PO |
又∵
| |PF1 |
| PF2| |
∴|
| PO |
∴|OP|=2a
当P点在x轴上时
∵|
| F1F2 |
| PF1 |
| PF2 |
∴经检验知也满足|OP|=2a
由以上得|OP|=2a
∴点p是在以O为圆心，以2a为半径的圆上．
∴动点P的轨迹是圆．
故选B．
点评：本题关键通过建立坐标系再通过以向量为载体考查圆的轨迹问题，解决此类问题的关键是熟练掌握向量的基本计算以及向量条件的转化．
练习册系列答案
名校课堂系列答案
相关题目
的两焦点，P是椭圆在第一象限弧上一点，且满足
·
＝1．过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点．
的两焦点，P是椭圆在第一象限弧上一点，且满足
·
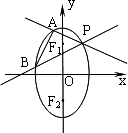
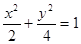＝1．过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点．
的两焦点，
是椭圆在第一象限弧上一点，且满足
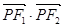=1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.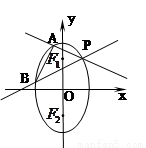
的两焦点，P是椭圆在第一象限弧上一点，且满足
=1，过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点，