题目内容
已知函数 对任意
对任意 都满足
都满足 ,且
,且 ,数列
,数列 满足:
满足: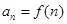 ,
,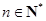 .
.
(Ⅰ)求 及
及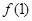 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若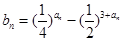 ,试问数列
,试问数列 是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.
是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.
 对任意
对任意 都满足
都满足 ,且
,且 ,数列
,数列 满足:
满足: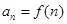 ,
,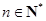 .
.(Ⅰ)求
 及
及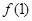 的值;
的值;(Ⅱ)求数列
 的通项公式;
的通项公式;(Ⅲ)若
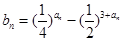 ,试问数列
,试问数列 是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.
是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.(Ⅰ) ,
, ,(Ⅱ)
,(Ⅱ) ,(Ⅲ)当
,(Ⅲ)当 ,即
,即 时,
时, 的最大项为
的最大项为 .当
.当 ,即
,即 时,
时, 的最小项为
的最小项为 .
.
 ,
, ,(Ⅱ)
,(Ⅱ) ,(Ⅲ)当
,(Ⅲ)当 ,即
,即 时,
时, 的最大项为
的最大项为 .当
.当 ,即
,即 时,
时, 的最小项为
的最小项为 .
.试题分析:(Ⅰ)对应抽象函数,一般方法为赋值法. 在
 中,取
中,取 ,得
,得 ,在
,在 中,取
中,取 ,得
,得 ,(Ⅱ)在
,(Ⅱ)在 中,令
中,令 ,
, ,得
,得 ,即
,即 .所以
.所以 是等差数列,公差为2,又首项
是等差数列,公差为2,又首项 ,所以
,所以 ,
,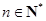 .(Ⅲ)研究数列
.(Ⅲ)研究数列 是否存在最大项和最小项,关键看通项公式的特征.令
是否存在最大项和最小项,关键看通项公式的特征.令 ,则
,则 ,显然
,显然 ,又因为
,又因为 ,所以当
,所以当 ,即
,即 时,
时, 的最大项为
的最大项为 .当
.当 ,即
,即 时,
时, 的最小项为
的最小项为
解:(Ⅰ)在
 中,取
中,取 ,得
,得 ,
,在
 中,取
中,取 ,得
,得 , 2分
, 2分(Ⅱ)在
 中,令
中,令 ,
, ,
,得
 ,即
,即 .
.所以
 是等差数列,公差为2,又首项
是等差数列,公差为2,又首项 ,所以
,所以 ,
,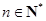 . 6分
. 6分(Ⅲ)数列
 存在最大项和最小项
存在最大项和最小项令
 ,则
,则 ,
,显然
 ,又因为
,又因为 ,
,所以当
 ,即
,即 时,
时, 的最大项为
的最大项为 .
.当
 ,即
,即 时,
时, 的最小项为
的最小项为 . 13分
. 13分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在
在 处取得最大值,则
处取得最大值,则



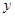 (万元)与处理量
(万元)与处理量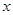 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: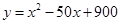 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为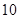 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴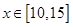 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;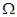 为平面直角坐标系
为平面直角坐标系 中的点集,从
中的点集,从 作
作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为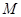 ,
, ,记点
,记点 ,点
,点 .如果
.如果 的取值范围是( )
的取值范围是( )



 的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是( )
的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是( )
 的函数
的函数 (
( )有两个单调区间,则实数
)有两个单调区间,则实数 ,
, ,
, 满足( )
满足( ) 且
且


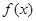 满足
满足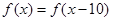 ,当
,当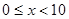 时,
时,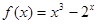 ,则函数
,则函数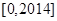 上的零点个数为( )
上的零点个数为( ) 立方米,且
立方米,且 . 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
. 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )


 与
与 ,若
,若 与
与 的交点在直线
的交点在直线 的两侧,
的两侧, 的取值范围是 ( )
的取值范围是 ( )


