题目内容
如图,F1、F2为椭圆 的左右焦点,P为椭圆上一点,且位于x轴上方,过点P作x轴的平行线交椭圆右准线于点M,连接MF2,
的左右焦点,P为椭圆上一点,且位于x轴上方,过点P作x轴的平行线交椭圆右准线于点M,连接MF2,(1)若存在点P,使PF1F2M为平行四边形,求椭圆的离心率e的取值范围;
(2)若存在点P,使PF1F2M为菱形;
①求椭圆的离心率;
②设A(a,0)、B(0,b),求证:以F1A为直径的圆经过点B.

【答案】分析:(1)先设P(x,y),利用椭圆的几何性质及平行四边形的性质得出P点横坐标的表达式,再结合椭圆的范围得出关于a,c的不等关系,即可求出椭圆的离心率e的取值范围;
(2)①根据椭圆的两种定义方法,构造关于离心率的关系式,即可求出答案;
②先写出以F1A为直径的圆方程,再证B(0,b)满足方程即可.
解答:解:(1)设P(x,y),则 ,
,
∵|PM|=|F1F2|=2c,
∴ ,
,
由 ;
;
(2)① ,
, ,
,
∵0<e<1,∴ ;
;
②以F1A为直径的圆方程为(x+c)(x-a)+y2=0,
下证B(0,b)满足方程,即-ac+b2=0…(*),
∵e2+e-1=0,
∴c2+ac-a2=0,
∴ac=a2-c2=b2,∴(*)成立,
∴以F1A为直径的圆经过点B.
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,考查了学生的运算能力.属中档题.
(2)①根据椭圆的两种定义方法,构造关于离心率的关系式,即可求出答案;
②先写出以F1A为直径的圆方程,再证B(0,b)满足方程即可.
解答:解:(1)设P(x,y),则
 ,
,∵|PM|=|F1F2|=2c,
∴
 ,
,由
 ;
;(2)①
 ,
, ,
,∵0<e<1,∴
 ;
;②以F1A为直径的圆方程为(x+c)(x-a)+y2=0,
下证B(0,b)满足方程,即-ac+b2=0…(*),
∵e2+e-1=0,
∴c2+ac-a2=0,
∴ac=a2-c2=b2,∴(*)成立,
∴以F1A为直径的圆经过点B.
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,考查了学生的运算能力.属中档题.

练习册系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C: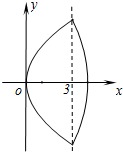 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: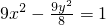 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;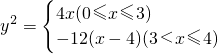 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 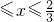 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: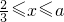 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.