题目内容
9.直线2x+3y+1=0关于直线x-y-1=0的对称直线方程为3x+2y=0.分析 在所求直线上任意取一点M(x,y),利用垂直、中点在轴上着2个条件,求得点M关于直线x-y-1=0的对称点M′的坐标,再根据点M′在直线2x+3y+1=0上,建立x、y的关系,可得所求直线的方程.
解答 解:在直线2x+3y+1=0关于直线x-y-1=0的对称直线上任意取一点M(x,y),
设点M关于直线x-y-1=0的对称点M′(x′,y′),则由$\left\{\begin{array}{l}{•\frac{y-y′}{x-x′}=-1}\\{2•\frac{x+x′}{2}+3\frac{y+y′}{2}+1=0}\end{array}\right.$,
可得x′=y+1,y′=x-1,即M′(y+1,x-1).
由M′在直线2x+3y+1=0上,可得2•(y+1)+3•(x-1)+1=0,即3x+2y=0,
故答案为:3x+2y=0.
点评 本题主要求一条直线关于另一直线的对称直线的方法,求一个点关于一条直线的对称点的方法,利用垂直、中点在轴上着2个条件,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
20.如图所示的程序框图,其功能是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等,则这样的x值有( )
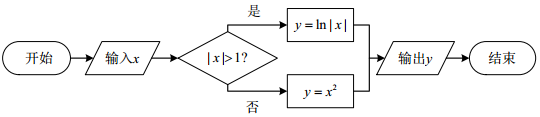

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.若直线y=kx+2(k∈R)与椭圆x2+$\frac{{y}^{2}}{m}$=1恒有交点,则实数m的取值范围为( )
| A. | (4,+∞) | B. | [4,+∞) | C. | (-∞,4) | D. | (-∞,4] |
18.已知函数f(x)=cos$\frac{x+2φ}{3}$(φ∈[-π,0])的图象关于原点对称,为了得到函数y=cos($\frac{π}{6}$+$\frac{x}{3}$)的图象,只需把函数f(x)的图象( )
| A. | 向左平移$\frac{2π}{3}$个单位 | B. | 向右平移$\frac{2π}{3}$个单位 | ||
| C. | 向左平移2π个单位 | D. | 向右平移2π个单位 |
19.函数y=xlnx在(0,5)上是( )
| A. | 单调增函数 | |
| B. | 单调减函数 | |
| C. | 在$({0,\frac{1}{e}})$上是增函数,在$({\frac{1}{e},5})$上是减函数 | |
| D. | 在$({0,\frac{1}{e}})$上是减函数,在$({\frac{1}{e},5})$上是增函数 |