Question

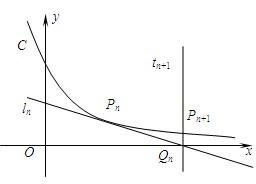点P_n（x_n，y_n）在曲线C：y=e^-x上，曲线C在点P_n处的切线l_n与x轴相交于点Q_n（x_n+1，0），直线t_n+1：x=x_n+1与曲线C相交于点P_n+1（x_n+1，y_n+1），（n=1，2，3，…）．由曲线C和直线l_n，t_n+1围成的图形面积记为S_n，已知x₁=1．
（Ⅰ）证明：x_n+1=x_n+1；
（Ⅱ）求S_n关于n的表达式；
（Ⅲ）记数列{S_n}的前n项之和为T_n，求证：

Tn+1

Tn

＜

xn+1

xn

（n=1，2，3，…）．

Answer 1

分析：（Ⅰ）对函数y=e^-x进行求导，推断出切线l_n的斜率，则可求得切线l_n的方程把y=0代入即可求得xQn=xn+1，即x_n+1=x_n+1．
（Ⅱ）根据根据x₁=1及（1）中的递推式可求得x_n，进而利用定积分的公式和性质求得答案．

解答：（Ⅰ）证明：因为y=e^-x，所以y'=-e^-x，
则切线l_n的斜率kn=-e-xn，所以切线l_n的方程
为y-yn=-e-xn(x-xn)，令y=0，
得xQn=xn+1，即x_n+1=x_n+1
（Ⅱ）解：因为x₁=1，所以x_n=n，
所以Sn=

∫

xn+1 xn

e-xdx-

1

2

(xn+1-xn)•yn=(-e-x)

|

n+1 n

-

1

2

×e-n=

(e-2)e-n

2e

，
（Ⅲ）Tn=

e-2

2e

（

1

e1

+

1

e2

+…+

1

en

）=

e-2

2e

（

1 e (1- 1 en )

1- 1 e

）=

e-2

2e(e-1)

（1-

1

en

）；

Tn+1

Tn

=

1- 1 en+1

1- 1 en

=1+

e-1

en+1-e

，
而

xn+1

xn

=

n+1

n

=1+

1

n

，
要证

Tn+1

Tn

＜

xn+1

xn

成立，只需证明

e-1

en+1-e

＜

1

n

即可；
即只要证明eⁿ⁺¹＞（e-1）n+e（10分）
证明；数学归纳法：
①当n=1时，显然（e-1）²＞0?e²＞2e-1?e²＞（e-1）+e成立
②假设n=k时，有e^k+1＞（e-1）k+e
当n=k+1时，e^k+2=e•e^k+1＞e[（e-1）k+e]
而e[（e-1）k+e]-[（e-1）（k+1）+e]=（e-1）²（k+1）＞0
∴e^k+2=e•e^k+1＞e[（e-1）k+e]＞（e-1）（k+1）+e
这说明n=k+1时不等式也成立，
故

Tn+1

Tn

＜

xn+1

xn

对一切正整数n都成立．

点评：本题主要考查了数列的递推式及定积分的性质与计算．考查了学生综合把握所学知识的能力．