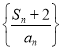题目内容
【题目】已知点![]() 为椭圆
为椭圆![]() 上一点,其中
上一点,其中![]() 为椭圆
为椭圆![]() 的离心率,椭圆
的离心率,椭圆![]() 的长轴长是短轴长的两倍.
的长轴长是短轴长的两倍.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() ,
,![]() (均不与点
(均不与点![]() 重合)是该椭圆上关于原点对称的两点,当
重合)是该椭圆上关于原点对称的两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
(1)将![]() 代入
代入![]() ,得
,得![]() ,椭圆
,椭圆![]() 的长轴长是短轴长的两倍,可得
的长轴长是短轴长的两倍,可得![]() ,联立方程,即可求得答案;
,联立方程,即可求得答案;
(2)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,![]() 的面积为1. 当直线
的面积为1. 当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,代入
,代入![]() ,求得
,求得![]() ,根据点到直线距离公式求得点
,根据点到直线距离公式求得点![]() 到直线
到直线![]() 的距离
的距离![]() ,结合均值不等式,即可求得答案.
,结合均值不等式,即可求得答案.
(1)将![]() 代入
代入![]() ,
,
得![]() ,即
,即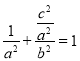 ,
,
从而得![]() .
.
又椭圆![]() 的长轴长是短轴长的两倍,
的长轴长是短轴长的两倍,
![]()
![]() ,
,
由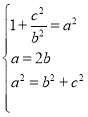 ,得
,得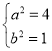 ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
易得![]() 的面积为1.
的面积为1.
②当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,代入
,代入![]()
并化简得![]() ,得
,得![]() ,
,
![]()
![]() .
.
由(1)易得![]() ,所以
,所以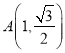 ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离
的距离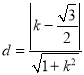 .
.
![]()
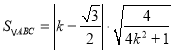
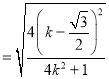
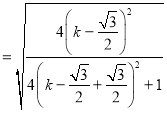
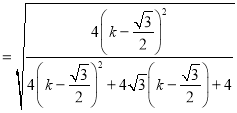 .
.
记![]() ,则有
,则有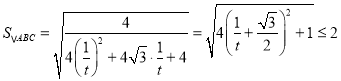 ,
,
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
故当![]() 的面积最大时,直线
的面积最大时,直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目
【题目】某科研小组为了研究一种治疗新冠肺炎患者的新药的效果,选50名患者服药一段时间后,记录了这些患者的生理指标![]() 和
和![]() 的数据,并统计得到如下的
的数据,并统计得到如下的![]() 列联表(不完整):
列联表(不完整):
|
| 合计 | |
| 12 | 36 | |
| 7 | ||
合计 |
其中在生理指标![]() 的人中,设
的人中,设![]() 组为生理指标
组为生理指标![]() 的人,
的人,![]() 组为生理指标
组为生理指标![]() 的人,他们服用这种药物后的康复时间(单位:天)记录如下:
的人,他们服用这种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,25
组:12,13,15,16,17,14,25
(Ⅰ)填写上表,并判断是否有95%的把握认为患者的两项生理指标![]() 和
和![]() 有关系;
有关系;
(Ⅱ)从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
附: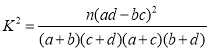 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |