题目内容
【题目】已知各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,且对任意n
,且对任意n![]() ,
,![]() 恒成立.
恒成立.
(1)求证:数列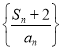 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,已知
,已知![]() ,
,![]() ,
,![]() (2<i<j)成等差数列,求正整数i,j.
(2<i<j)成等差数列,求正整数i,j.
【答案】(1)证明见解析;![]() (2)i=4,j=5
(2)i=4,j=5
【解析】
(1)根据题目所给递推关系式证得数列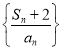 是等差数列,由此得到
是等差数列,由此得到![]() .利用
.利用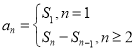 求得数列
求得数列![]() 的通项公式.
的通项公式.
(2)由(1)求得![]() 的表达式,由
的表达式,由![]() 成等差数列列方程,分成
成等差数列列方程,分成![]() 和
和![]() 两种情况进行分类讨论,由此求得整数
两种情况进行分类讨论,由此求得整数![]() .
.
(1)∵![]() ,
,
∴![]() ,
,
∵数列![]() 各项均为正数,∴
各项均为正数,∴![]() ,等式两边同时除以
,等式两边同时除以![]() ,
,
得![]() ,故数列
,故数列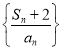 是等差数列,首项为2,公差为0,
是等差数列,首项为2,公差为0,
∴![]() ,即
,即![]() ①,
①,![]() ,求得
,求得![]() ,
,
∴![]() (n≥2)②,①﹣②得
(n≥2)②,①﹣②得![]() ,即
,即![]() ,
,
又![]() ,∴对任意n
,∴对任意n![]() ,数列
,数列![]() 是以2为首项,2为公比的等比数列
是以2为首项,2为公比的等比数列
故数列![]() 的通项公式为
的通项公式为![]() ;
;
(2)![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() (2<i<j)成等差数列,
(2<i<j)成等差数列,
∴![]() ,
,
变形得![]() (*),
(*),
①当![]() 时,
时,![]() ,
,
令![]() (i≥3),则
(i≥3),则![]() (i≥3),
(i≥3),
∴数列![]() 单调递减,故
单调递减,故![]() ,
,
∴![]() ,
,![]() ,故
,故![]() 时*式不成立,
时*式不成立,
②当![]() 时,*式转化为
时,*式转化为![]() ,解得i=4,故j=5.
,解得i=4,故j=5.

练习册系列答案
相关题目