题目内容

在等腰△ABC中，AB=AC，且sinB=
3
3
．
（Ⅰ）求cosA的值；
（Ⅱ）若|2
AB
+
AC
|=
11
，求|
AB
|．
分析：（Ⅰ）三角形的内角和为π，利用三角函数的诱导公式求值．
（Ⅱ）向量的模的平方等于向量的平方．
解答：解：（Ⅰ）在△ABC中，由A+2B=π得A=π-2B．
所以cosA=cos(π-2B)=-cos2B=2sin2B-1=-
1
3
．
（Ⅱ）由|2
AB
+
AC
|=
11
得4
AB
2+
AC
2+4
AB
•
AC
=11．
又|
AB
|=|
AC
|，
AB
•
AC
=|
AB
|•|
AC
|•cosA=-
1
3
|
AB
|2；
于是有5|
AB
|2-
4
3
|
AB
|2=11，解得|
AB
|=
3
．
答：（Ⅰ）cosA的值为-
1
3
；（Ⅱ）|
AB
|=
3
点评：本题考查向量的运算在解三角形中的应用．
练习册系列答案
相关题目
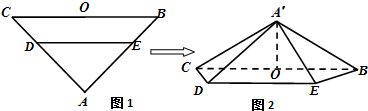如图1，在等腰△ABC中，∠A=90°，BC=6，D，E分别是AC，AB上的点，CD=BE=
2
，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱锥A′-BCDE，其中A′O=
3
．
（1）证明：A′O⊥平面BCDE；      
（2）求A′D与平面A′BC所成角的正弦值．
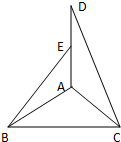如图，在等腰△ABC中，∠A=90°，BC=
2
，DA⊥AC，DA⊥AB，若DA=1，且E为DA的中点，求异面直线BE与CD所成角的余弦值．
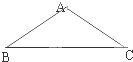如图，在等腰△ABC中，AB=AC=1，∠B=30°，则向量
AB
在向量
CA
上的投影等于（　　）
在三角形△ABC中，a，b，c分别是∠A，∠B，∠C的对应边，若asinA=bsinB，则三角形ABC是（　　）
如图1，在等腰△ABC中，∠A=90°，BC=6，D，E分别是AC，AB上的点，CD=BE=
2
，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱锥A′-BCDE．若A′O⊥平面BCDE，则A′D与平面A′BC所成角的正弦值等于（　　）
精英家教网
A、
2
3
B、
3
3
C、
2
2
D、
2
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网