题目内容
二次函数y=x2+ax+1,当x∈[2,3]时y>0恒成立,则a的取值范围是
- A.

- B.
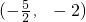
- C.
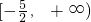
- D.

A
分析:由x∈[2,3]时y>0恒成立可得, 在x∈[3,4]恒成立,构造函数
在x∈[3,4]恒成立,构造函数  ,x∈[2,3]从而转化为a>g(x)max结合函数
,x∈[2,3]从而转化为a>g(x)max结合函数  =
=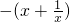 在x∈[2,3]单调性可求.
在x∈[2,3]单调性可求.
解答:∵二次函数y=x2+ax+1,当x∈[2,3]时y>0恒成立
∴ 在x∈[3,4]恒成立,
在x∈[3,4]恒成立,
令 ,x∈[2,3]即a>g(x)max
,x∈[2,3]即a>g(x)max
而 =
=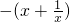 在x∈[2,3]单调递减,
在x∈[2,3]单调递减,
故g(x)在x=3时取得最大值-
则a的取值范围是
故选A.
点评:本题主要考查了函数恒成立问题,此类问题常构造函数,转化为求解函数的最值问题:a>f(x)(或a<f(x))恒成立?a>f(x)max(或a<f(x)min),体现了转化思想在解题中的应用.
分析:由x∈[2,3]时y>0恒成立可得,
 在x∈[3,4]恒成立,构造函数
在x∈[3,4]恒成立,构造函数  ,x∈[2,3]从而转化为a>g(x)max结合函数
,x∈[2,3]从而转化为a>g(x)max结合函数  =
=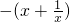 在x∈[2,3]单调性可求.
在x∈[2,3]单调性可求.解答:∵二次函数y=x2+ax+1,当x∈[2,3]时y>0恒成立
∴
 在x∈[3,4]恒成立,
在x∈[3,4]恒成立,令
 ,x∈[2,3]即a>g(x)max
,x∈[2,3]即a>g(x)max而
 =
=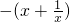 在x∈[2,3]单调递减,
在x∈[2,3]单调递减,故g(x)在x=3时取得最大值-

则a的取值范围是

故选A.
点评:本题主要考查了函数恒成立问题,此类问题常构造函数,转化为求解函数的最值问题:a>f(x)(或a<f(x))恒成立?a>f(x)max(或a<f(x)min),体现了转化思想在解题中的应用.

练习册系列答案
相关题目
