题目内容
△ABC中，若F依次是线段AB最靠近B的三等分点，则以| CB |
| e1 |
| CA |
| e2 |
| CF |
| 3 |
| 4 |
分析：由题意有可得
=
+
=
+
(
-
)，化简得出结果； 利用诱导公式 把函数化为 y=-cos2x，
从而得到此函数为偶函数．
| CF |
| CA |
| AF |
| e2 |
| 2 |
| 3 |
| e1 |
| e2 |
从而得到此函数为偶函数．
解答：解：△ABC中，
=
+
=
+
=
+
(
-
)=
+
．
函数y=sin2(x+
π)=sin（2x+
）=-cos2x，是个偶函数．
故答案为：
+
；偶函数．
| CF |
| CA |
| AF |
| CA |
| 2 |
| 3 |
| AB |
| e2 |
| 2 |
| 3 |
| e1 |
| e2 |
| 2 |
| 3 |
| e1 |
| 1 |
| 3 |
| e2 |
函数y=sin2(x+
| 3 |
| 4 |
| 3π |
| 2 |
故答案为：
| 2 |
| 3 |
| e1 |
| 1 |
| 3 |
| e2 |
点评：本题考查两个向量的加减法的法则，以及其几何意义，判断函数的奇偶性，诱导公式的应用，把函数化为 y=-cos2x，
是解题的关键．
是解题的关键．
练习册系列答案
相关题目
=e1,
=e2为基底时，
=_________________. 
，
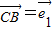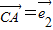为基底时，向量
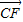= ；函数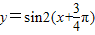
的奇偶性为 ．