题目内容

已知
a
= (2cosx，1)、
b
=(cosx，
3
sin2x+m)，f(x)=
a
•
b
．
（1）求函数在[0，π]上的单调增区间；
（2）当x∈[0，
π
3
]时，f（x）的最大值为6，求实数m的值．
分析：（1）利用两个向量的数量积公式，两角和的正弦公式，化简f（x） 的 解析式为2sin（2x+
π
6
）+m+1，由
 2kπ-
π
2
≤2x+
π
6
≤2kπ+
π
2
，k∈z，求出函数在[0，π]上的增区间．
（2）当x∈[0，
π
3
]时，2x+
π
6
∈[
π
6
，
5π
6
]，故当2x+
π
6
=
π
2
，f（x）=2+m+1 的值为6，由此求得m 值
解答：解：（1）f(x)=
a
•
b
=(2cosx ，1) • (cosx，
3
sin2x+m)=2cos2x+
3
sin2x + m 
=cos2x+
3
sin2x+m+1=2sin（2x+
π
6
）+m+1．
由   2kπ-
π
2
≤2x+
π
6
≤2kπ+
π
2
，k∈z，可得  kπ-
π
3
≤x≤kπ+
π
6
，故函数在[0，π]上的增区间为
[0，
π
6
]，[
2π
3
，π]．
（2）当x∈[0，
π
3
]时，2x+
π
6
∈[
π
6
，
5π
6
]，故当2x+
π
6
=
π
2
，即 x=
π
6
 时，
f（x）=2+m+1 的值为6，∴m=3．
点评：本题考查两个向量的数量积公式，两角和的正弦公式，正弦函数的单调性，三角函数的最值，求出f（x） 的解析式，
是解题的关键．
练习册系列答案
相关题目
已知A(2cosα，
3
sinα)、B(2cosβ，
3
sinβ)、C(-1，0)是平面上三个不同的点，若存在实数λ，使得
CA
=λ
BC
，则λ的取值范围是
 
．
设已知
a
=(2cos
α+β
2
，sin
α-β
2
)，
b
=(cos
α+β
2
，3sin
α-β
2
)，其中α、β∈（0，π）．
（1）若α+β=
2π
3
，且
a
=2
b
，求α、β的值；
（2）若
a
•
b
=
5
2
，求tanαtanβ的值．
已知
a
=(2cosα，2sinα)，
b
=(cosβ，sinβ)，0＜α＜β＜2π．
（Ⅰ）若
a
⊥
b
，求|
a
-2
b
|的值；
（Ⅱ）设
c
=(2，0)，若
a
+2
b
=
c
，求α，β的值．
(理)设A={x|x≠kπ+,k∈Z},已知a=(2cos,sin),b=(cos,3sin),其中α、β∈A,

(1)若α+β=,且a=2b,求α,β的值;

(2)若a·b=,求tanαtanβ的值.

(文)已知函数f(x)=-x2+4,设函数F(x)=

(1)求F(x)的表达式;

(2)解不等式1≤F(x)≤2;

(3)设mn＜0,m+n＞0,判断F(m)+F(n)能否小于0?

已知a=2cos（x+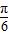）dx，则二项式（x2+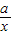）5的展开式中x的系数为    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网