题目内容

已知A(2cosα，
3
sinα)、B(2cosβ，
3
sinβ)、C(-1，0)是平面上三个不同的点，若存在实数λ，使得
CA
=λ
BC
，则λ的取值范围是
 
．
分析：由得
CA
=λ
BC
得A，B，C三点公线，由A，B的坐标不难发现：A，B均为椭圆
x2
4
+ 
y2
3
=1上的点，C为椭圆的左焦点，固画出图象，再结构椭圆的性质不难求出满足条件的λ的取值范围．
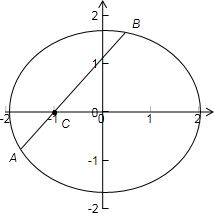解答：精英家教网解：∵A(2cosα，
3
sinα)、B(2cosβ，
3
sinβ)、C(-1，0)
A，B均为椭圆
x2
4
+ 
y2
3
=1上的点，C为椭圆的左焦点，如图示，
由椭圆的性质我们可得：
当A点落在椭圆的左顶点，B点落在椭圆的右顶点上时，λ有最小值
1
3
；
当A点落在椭圆的右顶点，B点落在椭圆的左顶点上时，λ有最大值3．
故λ的取值范围为：[
1
3
，3]，
故答案为：[
1
3
，3]．
点评：本题考查的主要知识点是椭圆的基本性质，但题目中并未直接给出点在椭圆上的已知条件，而是需要我们根据点坐标的特点，自己进行判定，如果错把本题的主要考查点当成是向量平行的坐标运算，就会导致花费大量的时间，而无法解决问题．
练习册系列答案
相关题目
设已知
a
=(2cos
α+β
2
，sin
α-β
2
)，
b
=(cos
α+β
2
，3sin
α-β
2
)，其中α、β∈（0，π）．
（1）若α+β=
2π
3
，且
a
=2
b
，求α、β的值；
（2）若
a
•
b
=
5
2
，求tanαtanβ的值．
已知
a
=(2cosα，2sinα)，
b
=(cosβ，sinβ)，0＜α＜β＜2π．
（Ⅰ）若
a
⊥
b
，求|
a
-2
b
|的值；
（Ⅱ）设
c
=(2，0)，若
a
+2
b
=
c
，求α，β的值．
(理)设A={x|x≠kπ+,k∈Z},已知a=(2cos,sin),b=(cos,3sin),其中α、β∈A,

(1)若α+β=,且a=2b,求α,β的值;

(2)若a·b=,求tanαtanβ的值.

(文)已知函数f(x)=-x2+4,设函数F(x)=

(1)求F(x)的表达式;

(2)解不等式1≤F(x)≤2;

(3)设mn＜0,m+n＞0,判断F(m)+F(n)能否小于0?

已知a=2cos（x+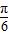）dx，则二项式（x2+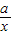）5的展开式中x的系数为    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网