题目内容
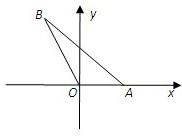 如图,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为
如图,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为| 3π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
(Ⅰ)用θ表示点B的坐标及|OA|;
(Ⅱ)若tanθ=-
| 4 |
| 3 |
| OA |
| OB |
分析:(Ⅰ)由三角函数的定义,得点B的坐标;在△AOB中利用正弦定理求出|OA|长.
(Ⅱ)利用向量的数量积公式等于向量的模乘以它们的夹角余弦乘积及三角函数的诱导公式求出.
(Ⅱ)利用向量的数量积公式等于向量的模乘以它们的夹角余弦乘积及三角函数的诱导公式求出.
解答:(Ⅰ)解:由三角函数的定义,得点B的坐标
为(2cosθ,2sinθ).
在△AOB中,|OB|=2,∠BAO=
, ∠B=π-
-θ=
-θ,
由正弦定理,得
=
,
即
=
,
所以|OA|=2
sin(
-θ).
(Ⅱ)解:由(Ⅰ)得
•
=|
|•|
|•cosθ=4
sin(
-θ)•cosθ,
因为tanθ=-
, θ∈(
,
),
所以sinθ=
, cosθ=-
,
又sin(
-θ)=sin
•cosθ-cos
•sinθ
=
•(-
)-(-
)•
=
,
所以
•
=4
•
•(-
)=-
.
为(2cosθ,2sinθ).
在△AOB中,|OB|=2,∠BAO=
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
由正弦定理,得
| |OB| | ||
sin
|
| |OA| |
| sin∠B |
即
| 2 | ||||
|
| |OA| | ||
sin(
|
所以|OA|=2
| 2 |
| 3π |
| 4 |
(Ⅱ)解:由(Ⅰ)得
| OA |
| OB |
| OA |
| OB |
| 2 |
| 3π |
| 4 |
因为tanθ=-
| 4 |
| 3 |
| π |
| 2 |
| 3π |
| 4 |
所以sinθ=
| 4 |
| 5 |
| 3 |
| 5 |
又sin(
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
=
| ||
| 2 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| ||
| 10 |
所以
| OA |
| OB |
| 2 |
| ||
| 10 |
| 3 |
| 5 |
| 12 |
| 25 |
点评:本题考查三角函数的定义;考查三角函数的正弦定理;考查向量的数量积;考查三角函数的诱导公式.

练习册系列答案
相关题目
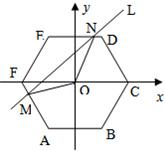 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
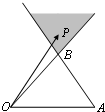 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是