题目内容
盒子里装有16只球,其中6只是玻璃球,另外10只是木质球.而玻璃球中有2只是红色的,4只是蓝色的;木质球中有3只是红色的,7只是蓝色的,现从中任取一只球,如果已知取到的是蓝色的球,求这个球是玻璃球的概率.

解析解:设A表示“任取一球,是玻璃球”,B表示“任取一球,是蓝色的球”,则AB表示“任取一球是蓝色玻璃球”.
P(B)= ,P(AB)=
,P(AB)= ,
,
P(A|B)= =
= .
.

练习册系列答案
相关题目
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 | x | 0.45 |
| 10 | 35 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 | z | |
| 10 | | 0.35 |
| 合计 | 80 | 1 |
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).
 ,B级考试合格的概率为
,B级考试合格的概率为 .假设各级考试成绩合格与否均互不影响.
.假设各级考试成绩合格与否均互不影响. ,求
,求 .
.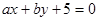 与圆
与圆 相切的概率;
相切的概率; 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率. 、
、 两个盒子中分别装有标记为
两个盒子中分别装有标记为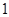 ,
, ,
, ,
, 的大小相同的四个小球,甲从
的大小相同的四个小球,甲从 表示事件“甲抽到标号为
表示事件“甲抽到标号为 的小球,乙抽到标号为
的小球,乙抽到标号为 的小球”,试写出所有可能的事件;
的小球”,试写出所有可能的事件; ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数. 、
、 、
、 三道工序加工而成的,
三道工序加工而成的, 、
、 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场. 袋食品,求这2袋食品都为废品的概率;
袋食品,求这2袋食品都为废品的概率; 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次. 的分布列和数学期望.
的分布列和数学期望.