题目内容
【题目】若函数![]() 在区间
在区间![]()
![]() 内恰有2019个零点,则
内恰有2019个零点,则![]() ________
________
【答案】![]()
【解析】
根据零点的定义可知,方程![]() ,即
,即![]()
在![]() 内有有2019个根,显然
内有有2019个根,显然![]() 不满足方程,所以
不满足方程,所以![]()
令![]() ,再研究直线
,再研究直线![]() 与函数
与函数![]() 的交点个数,即可解出.
的交点个数,即可解出.
令![]() ,即有
,即有![]() ,因为
,因为![]() 不满足方程,所以
不满足方程,所以![]() ,令
,令![]() ,∴
,∴![]() .∵函数
.∵函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递增,由图象可知,直线
上递增,由图象可知,直线![]() 与函数
与函数![]() 的图象至少有一个交点.
的图象至少有一个交点.
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象只有一个交点,此时
的图象只有一个交点,此时![]() ,
,![]() 在一个周期
在一个周期![]() 内的
内的![]() 上有两个解,所以在区间
上有两个解,所以在区间![]()
![]() 内不可能有奇数个解;
内不可能有奇数个解;
当![]() 时,同理可得,在区间
时,同理可得,在区间![]()
![]() 内不可能有奇数个解;
内不可能有奇数个解;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有两个交点,一个
的图象有两个交点,一个![]() ,一个
,一个![]() ,所以
,所以![]() 在一个周期
在一个周期![]() 内,
内,![]() 有两个解,
有两个解,![]() 有两个解,所以在区间
有两个解,所以在区间![]()
![]() 内不可能有奇数个解;
内不可能有奇数个解;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有两个交点,一个
的图象有两个交点,一个![]() ,一个
,一个![]() ,所以
,所以![]() 在一个周期
在一个周期![]() 内,
内,![]() 有两个解,
有两个解,![]() 有一个解,即一个周期
有一个解,即一个周期![]() 内有三个解,所以
内有三个解,所以![]() ,即
,即![]() .
.
当![]() 时,同理可得,
时,同理可得,![]() .
.
故答案为:![]() .
.
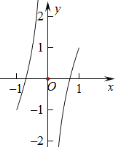

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目