题目内容

解析、解法一:(1)证明:取PC中点M,连结ME、MF,则MF∥CD,MF=![]() CD.
CD.
又AE∥CD,AE=![]() CD, ∴AE∥MF且AE=MF.
CD, ∴AE∥MF且AE=MF.
∴四边形AFME是平行四边形.∴AF∥EM.
∵AF![]() 平面PCE, ∴AF∥平面PCE. 4分
平面PCE, ∴AF∥平面PCE. 4分
(2)解:∵PA⊥平面AC,CD⊥AD,
∴CD⊥PD. ∴∠PDA是二面角P―CD―B的平面角,即∠PDA=45°.
∴△PAD是等腰直角三角形.
∴AF⊥PD.又AF⊥CD,
∴AF⊥平面PCD,而EM∥AF,
∴EM⊥平面PCD. 又EM![]() 平面PEC,
平面PEC,
∴面PEC⊥面PCD.
在平面PCD内过F作FH⊥PC于H,则FH就是点F到平面PCE的距离.
由已知,PD=2![]() ,PF=
,PF=![]() ,PC=
,PC=![]() ,△PFH∽△PCD,
,△PFH∽△PCD,
∴![]() =
=![]() . ∴FH=
. ∴FH=![]() . 8分
. 8分
(3)解:∵PA⊥平面ABCD,
∴AC是PC在底面上的射影. ∴∠PCA就是PC与底面所成的角.
由(2)知PA=2,PC=![]() , ∴sin∠PCA=
, ∴sin∠PCA=![]() =
=![]() ,
,
即PC与底面所成的角是arcsin![]() . 12分
. 12分

解法二:(1)证明:取PC中点M,连结EM,
∵![]() =
=![]() +
+![]() =
=![]() +
+![]()
![]() =
=![]() +
+![]() (
(![]() +
+![]() )=
)=![]() +
+![]()
![]() +
+![]()
=![]() +
+ ![]() +
+![]() =
=![]() ,
,
∴AF∥EM.又EM![]() 平面PEC,AF
平面PEC,AF![]() 平面PEC,
平面PEC,
∴AF∥平面PEC. 4分
(2)解:以A为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为x、y、z轴建立坐标系.
所在直线为x、y、z轴建立坐标系.
∵PA⊥平面AC,CD⊥AD, ∴CD⊥PD.
∴∠PDA是二面角P―CD―B的平面角,即∠PDA=45°.
∴A(0,0,0)、P(0,0,2)、D(0,2,0)、F(0,1,1)、E(![]() ,0,0)、C(3,2,0).
,0,0)、C(3,2,0).
设平面PCE的法向量为n=(x,y,z),则n⊥![]() ,n⊥
,n⊥![]() ,而
,而![]() =(-
=(-![]() ,0,2),
,0,2),![]() =(
=(![]() ,2,0),
,2,0),
∴-![]() x+2z=0,且
x+2z=0,且![]() x+2y=0. 解得y=-
x+2y=0. 解得y=-![]() x ,z=
x ,z=![]() x.
x.
取x=4,得n=(4,-3,3).
又![]() =(0,1,-1),故点F到平面PCE的距离为
=(0,1,-1),故点F到平面PCE的距离为
d=![]() =
=![]() =
=![]() . 8分
. 8分
(3)解: ∵PA⊥平面ABCD, ∴AC是PC在底面上的射影.
∴∠PCA就是PC与底面所成的角.![]() =(-3,-2,0),
=(-3,-2,0),![]() =(-3,-2,2).
=(-3,-2,2).
∴cos∠PCA=![]() =
=![]() , sin∠PCA=
, sin∠PCA=![]() =
=![]() ,
,
即PC与底面所成的角是arccos![]() . 12分
. 12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案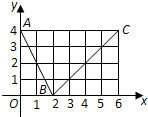 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=