题目内容
对于x∈R,不等式2x2-a
+3>0恒成立,则实数a的取值范围是
______.
| x2+1 |
2x2-a
+3>0恒成立,
即a<
恒成立,
下面只要求y=
的最小值即可,
令
=t(t≥1)则x2=t2-1,
所以y=
=2t+
,
∵y=2t+
在【1,+∞)单增,
所以当t=1时,y有最小值3,
所以a<3,
故答案为:a<3.
| x2+1 |
即a<
| 2x2+3 | ||
|
下面只要求y=
| 2x2+3 | ||
|
令
| x2+1 |
所以y=
| 2t2+1 |
| t |
| 1 |
| t |
∵y=2t+
| 1 |
| t |
所以当t=1时,y有最小值3,
所以a<3,
故答案为:a<3.

练习册系列答案
相关题目
 =
= ,变换T的矩阵为A=
,变换T的矩阵为A= ,平面上的点P(1,1)在变换T
,平面上的点P(1,1)在变换T 与圆
与圆 (
( >0)相交于A、B两点,设
>0)相交于A、B两点,设
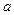 2+
2+ 2恒成立,试求2
2恒成立,试求2 =
= ,变换T的矩阵为A=
,变换T的矩阵为A= ,平面上的点P(1,1)在变换T
,平面上的点P(1,1)在变换T 与圆
与圆 (
( >0)相交于A、B两点,设
>0)相交于A、B两点,设 2+
2+ 2恒成立,试求2
2恒成立,试求2